题目内容
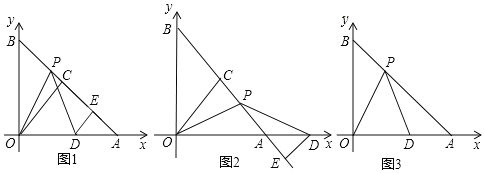
【题目】如图,在平面直角坐标系中,![]() 的三个顶点分别为
的三个顶点分别为![]() ,
,![]() ,
,![]() .
.
![]() 把
把![]() 向上平移
向上平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
![]() 已知点
已知点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,请画出直线
成轴对称,请画出直线![]() 及
及![]() 关于直线
关于直线![]() 对称的
对称的![]() .
.
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 距离之和最小,请直接写出
距离之和最小,请直接写出![]() 点的坐标.
点的坐标.
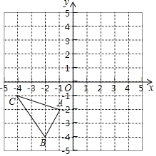
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
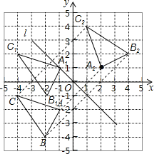
(1) 根据图形平移的性质画出△A1B1C1;
(2)连接AA1,再作AA1的垂直平分线,即为所求对称轴l,再根据两点关于直线对称的性质得到B2,C2,依次连接即可;
(3)作点C关于x轴对称的点![]() ,连接
,连接![]() 交x轴于一点即为点P,写出点P的坐标即可.
交x轴于一点即为点P,写出点P的坐标即可.
![]() 如图,
如图,![]() 即为所求;
即为所求;
![]() 如图,
如图,![]() 和直线
和直线![]() 即为所求.
即为所求.
(3)作点C关于x轴对称的点![]() ,连接
,连接![]() 交x轴于一点即为点P,如图所示:
交x轴于一点即为点P,如图所示:
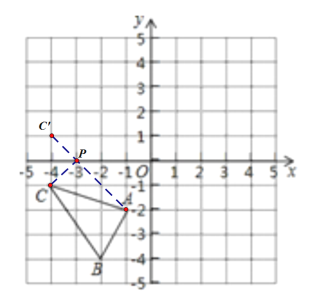
点C的坐标为(-4,-1)关于x轴对称的点![]() (-4,1),
(-4,1),
设直线AC’的函数的解析式y=kx+b,且点A(-1,-2),![]() 在直线A
在直线A![]() 上,
上,
![]() 解得
解得![]() ,
,
所以直线AC’的函数的解析式为![]() ,
,
设y=0,则x=-3,
即点P的坐标为(0,-3).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某超市购进一种水果进行销售,购进情况和销售情况见下表:
项目 | 购进资金 单位:元 | 进货价 单位:元/kg | 销售定价 单位:元/kg | 销售情况 | 水果重量 单位:kg |
第一次 | 6000 | m | 16 | 按定价全部售完 | 第二次是第一次的两倍 |
第二次 | 13000 | m+1 | 16 | 按定价售出一部分后,余下的400kg按定价的7折售完 |
(1)第二次的进货价是多少元/kg?
(2)超市在这两次销售中共盈利多少元?