题目内容
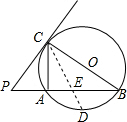
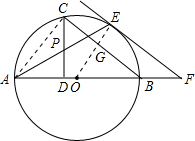
AB为⊙O的直径，C为弧AE的中点，CD⊥AB于D，AE交CD于点P，边接CB，过E作EF∥BC，交AB的延长线于F．
（1）求证：PA=PC．
（2）当E点在什么位置时，EF是⊙O的切线？
（1）求证：PA=PC．
（2）当E点在什么位置时，EF是⊙O的切线？
（1）证明：∵CD⊥AB，
∴∠ACD+∠CAD=90°，∠CAD+∠ABC=90°，
∴∠ACD=∠ABC，
∵C为
的中点，
∴
=
，
∴∠CAE=∠ABC，
∴∠ACD=∠CAE，
则PA=PC；
（2）当E为
中点时，EF为圆O的切线，理由为：
若E为
中点，连接OE，由垂径定理得到OE⊥BC，
∵BC∥EF，
∴OE⊥EF，
∴EF为圆O的切线．
∴∠ACD+∠CAD=90°，∠CAD+∠ABC=90°，
∴∠ACD=∠ABC，
∵C为
 |
| AE |
∴
|
| AC |
|
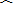| EC |
∴∠CAE=∠ABC，
∴∠ACD=∠CAE，
则PA=PC；
（2）当E为
|
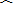| BC |
若E为
|
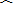| BC |
∵BC∥EF，
∴OE⊥EF，
∴EF为圆O的切线．
练习册系列答案
相关题目
