题目内容
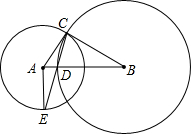
如图，EB、EC是⊙O的两条切线，B、C为切点，A是⊙O上的任意一点，若∠A=70°，则∠E=______．
连接OB，OC．
则∠BOC=2∠A=2×70=140°，
∵EB、EC是⊙O的两条切线，
∴∠EBO=∠ECO=90°，
∴∠E=360°-∠BOC-∠EBO-∠ECO=360°-140°-90°-90°=40°．
故答案是：40°．
则∠BOC=2∠A=2×70=140°，
∵EB、EC是⊙O的两条切线，
∴∠EBO=∠ECO=90°，
∴∠E=360°-∠BOC-∠EBO-∠ECO=360°-140°-90°-90°=40°．
故答案是：40°．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
△CPQ进行研究．
点E，连接AF．