题目内容
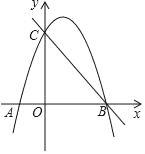
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B(A左B右),与y轴交于C,直线y=﹣x+5经过点B、C.
x2+bx+c与x轴交于A、B(A左B右),与y轴交于C,直线y=﹣x+5经过点B、C.
(1)求抛物线的解析式;
(2)点P为第二象限抛物线上一点,设点P横坐标为m,点P到直线BC的距离为d,求d与m的函数解析式;
(3)在(2)的条件下,若∠PCB+∠POB=180°,求d的值.
【答案】(1)y=﹣![]() x2+
x2+![]() x+5(2)d=
x+5(2)d=![]() m2﹣
m2﹣![]() m(﹣2<m<0)(3)
m(﹣2<m<0)(3)![]()
【解析】
(1)首先求出B、C两点坐标,再利用待定系数法即可解决问题;
(2)如图1中,作PE⊥BC于E,作PF∥AB交BC于F.只要证明△PEF是等腰直角三角形,想办法求出PF(用m表示),即可解决问题;
(3)首先证明O、B、C、P四点共圆,推出∠CPB=∠COB=90°,可得PH=![]() BC=
BC=![]() ,由P(m,﹣
,由P(m,﹣![]() m2+
m2+![]() m+5),H(
m+5),H(![]() ,
,![]() ),可得(m﹣
),可得(m﹣![]() )2+(﹣
)2+(﹣![]() m2+
m2+![]() m+5﹣
m+5﹣![]() )2=
)2=![]() ,解方程去m,再利用(2)中结论即可解决问题.
,解方程去m,再利用(2)中结论即可解决问题.
(1)∵直线y=﹣x+5经过点B、C,
∴B(5,0),C(0,5),
把B、C坐标代入y=﹣![]() x2+bx+c得到:
x2+bx+c得到: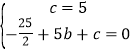 ,
,
解得![]() ,
,
∴二次函数的解析式为y=﹣![]() x2+
x2+![]() x+5;
x+5;
(2)如图1中,作PE⊥BC于E,作PF∥AB交BC于F.

∵P(m,﹣![]() m2+
m2+![]() m+5),
m+5),
∵PF∥AB,
∴点F的纵坐标为﹣![]() m2+
m2+![]() m+5,
m+5,
则有﹣![]() m2+
m2+![]() m+5=﹣x+5,
m+5=﹣x+5,
∴x=![]() m2﹣
m2﹣![]() m,
m,
∴PF=![]() m2﹣
m2﹣![]() m﹣m=
m﹣m=![]() m2﹣
m2﹣![]() m,
m,
∵OB=OC,∠BOC=90°,
∴∠EFP=∠OBC=45°,∵PE⊥EF,
∴△PEF是等腰直角三角形,
∴d=PE=![]() PF=
PF=![]() m2﹣
m2﹣![]() m(﹣2<m<0);
m(﹣2<m<0);
(3)如图2中,取BC的中点H,连接PH.

∵∠PCB+∠POB=180°,
∴O、B、C、P四点共圆,
∴∠CPB=∠COB=90°,
∴PH=![]() BC=
BC=![]() ,
,
∵P(m,﹣![]() m2+
m2+![]() m+5),H(
m+5),H(![]() ,
,![]() ),
),
∴(m﹣![]() )2+(﹣
)2+(﹣![]() m2+
m2+![]() m+5﹣
m+5﹣![]() )2=
)2=![]() ,
,
整理得:m(m﹣5)(m2﹣m﹣2)=0,
解得m=0或5或﹣1或2,
∵P在第二象限,
∴m=﹣1,
∴d=![]() m2﹣
m2﹣![]() m=
m=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案