题目内容
【题目】如图,△ABC和△DEF关于点O成中心对称.
(1)作出它们的对称中心O,并简要说明作法;
(2)若AB=6,AC=5,BC=4,求△DEF的周长;
(3)连接AF,CD,试判断四边形ACDF的形状,并说明理由.
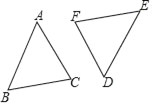
【答案】(1)答案见解析;(2)14;(3)平行四边形.
【解析】
(1)根据中心对称的性质,对称中心在线段AD和CF上,则连结AD和CF,它们的交点即为对称中心O;
(2)根据中心对称的两个三角形全等可得到△DEF各边的长,然后计算△DEF的周长;
(3)根据中心对称的性质得OA=OD,OC=OF,则根据平行四边形的判定方法可判断四边形ACDF为平行四边形.
(1)如图,点O为所作;

(2)∵△ABC和△DEF关于点O成心对称,∴△ABC≌△DEF,∴DF=AC=5,DE=AB=6,EF=BC=3,∴△DEF的周长=3+5+6=14;
(3)四边形ACDF为平行四边形.理由如下:
∵△ABC和△DEF关于点O成心对称,∴OA=OD,OC=OF,∴四边形ACDF为平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目