题目内容
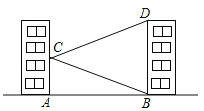
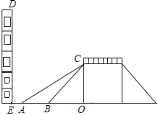
【题目】如图是某一过街天桥的示意图,天桥高![]() 为
为![]() 米,坡道倾斜角
米,坡道倾斜角![]() 为
为![]() ,在距
,在距![]() 点
点![]() 米处有一建筑物
米处有一建筑物![]() .为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角
.为方便行人上下天桥,市政部门决定减少坡道的倾斜角,但要求建筑物与新坡角![]() 处之间地面要留出不少于
处之间地面要留出不少于![]() 米宽的人行道.
米宽的人行道.
![]() 若将倾斜角改建为
若将倾斜角改建为![]() (即
(即![]() ),则建筑物
),则建筑物![]() 是否要拆除?(
是否要拆除?(![]() )
)
![]() 若不拆除建筑物
若不拆除建筑物![]() ,则倾斜角最小能改到多少度(精确到
,则倾斜角最小能改到多少度(精确到![]() )?
)?
【答案】(1)建筑物![]() 要拆除;(2)倾斜角最小能改到
要拆除;(2)倾斜角最小能改到![]() .
.
【解析】
(1)分别在△CAO和△CBO中,求出AO、BO的长度,最后比较AO+3与OE的长度,进行判断;
(2)若不拆除建筑物DE,则OA最长可以是113=8m,在Rt△CAO中,求出∠CAO的度数.
解:![]() 当
当![]() 时,
时,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∵![]() ,因此建筑物
,因此建筑物![]() 要拆除;
要拆除;
![]() 若不拆除建筑物
若不拆除建筑物![]() ,则
,则![]() 最长可以是
最长可以是![]() ,
,
在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,
因此倾斜角最小能改到![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】某商场经营某种品牌的计算器,购进时的单价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是600个,而销售单价每上涨1元,就会少售出10个.
(1)不妨设该种品牌计算器的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y个和销售该品牌计算器获得利润w元,并把结果填写在表格中:
销售单价(元) | x(x>30) |
销售量y(个) |
|
销售计算器获得利润w(元) |
|
(2)在第(1)问的条件下,若计算器厂规定该品牌计算器销售单价不低于35元,且商场要完成不少于500个的销售任务,求:商场销售该品牌计算器获得最大利润是多少?