��Ŀ����
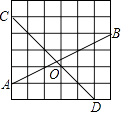
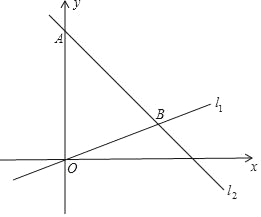
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�ڣ���A������Ϊ��0��8��������ԭ���ֱ��l1�뾭����A��ֱ��l2�ཻ�ڵ�B����B����Ϊ��6��2����
��1��ֱ��д��ֱ��l1�ı���ʽ�� ����l2�ı���ʽ�� ����
��2����CΪ�߶�0B��һ���㣨��C�����0��B�غϣ�����CD��y�ύֱ��l2�ڵ�D��
�����C�ĺ�����Ϊ3�����D������Ϊ�� ����
�����C�ĺ�����Ϊm�����D������Ϊ�� �������ú�m�Ĵ���ʽ��ʾ����
�������������£���CD=2����m��ֵΪ�� ����
���𰸡���1��y=![]() x��y=��x+8����2����D��3��5������D��m����m+8������
x��y=��x+8����2����D��3��5������D��m����m+8������![]() ��
��
��������
(1)����ֱ��l1�ı���ʽΪy=k1x����ֱ��l2�ı���ʽΪy=k2x+b����������뼴����������ʽ��
(2)�٢ڸ��ݵ�C��ֱ��l1�ϣ��ѵ�C�ĺ��������ֱ��l1�ı���ʽ���ɵó�C�����꣬����CD��y�ᣬ�ٸ��ݵ�D��ֱ��l2�ϼ��ɵó���D�ĺ����꣬�����ó����ۣ��۸���CD=2�з��̼��ɵõ����ۣ�
(1)��ֱ��l1�ı���ʽΪy=k1x��������6��2����6k1=2��k1=![]() ��
��
��y=![]() x��
x��
��ֱ��l2�ı���ʽΪy=k2x+b��������A��0��8����B��6��2����
��![]() ��
��
���![]() ��
��
��ֱ��l2�ı���ʽΪ��y=��x+8��
(2)��ͼ��
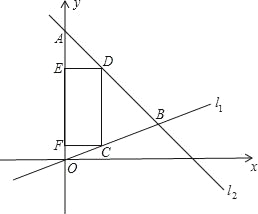
�١ߵ�C��ֱ��l1�ϣ��ҵ�C�ĺ�����Ϊ3��
��y=1��
���C��������3��1����
��CD��y�ᣬ
���D�ĺ�����Ϊ3��
�ߵ�D��ֱ��l2�ϣ�
��y=��3+8=5��
��D��3��5����
�ڡߵ�C��ֱ��l1�ϣ��ҵ�C�ĺ�����Ϊm��
��y=![]() m��
m��
���C��������m��![]() m����
m����
��CD��y�ᣬ
���D�ĺ�����Ϊm��
�ߵ�D��ֱ��l2�ϣ�
��y=��m+8��
��D��m����m+8����
�ۡ�CD=2��
����m+8��![]() m=2��
m=2��
��ã�m=![]() ��
��