题目内容
【题目】将背面是质地、图案完全相同,正面分别标有数字-2,-1,1,2的四张卡片洗匀后,背面朝上放置在桌面上.随机抽取一张卡片,将抽取的第一张卡片上的数字作为横坐标,第二次再从剩余的三张卡片中随机抽取一张卡片,将抽取的第二张卡片上的数字作为纵坐标.
(1)请用列表法或画树状图法求出所有可能的点的坐标;
(2)求出点在x轴上方的概率.
【答案】(1)列表或画树状图见解析,所有可能的点的坐标为(-1,-2),(1,-2),(2,-2),(-2,-1),(1,-1),(2,-1),(-2,1),(-1,1),(2,1),(-2,2),(-1,2),(1,2);(2)点在x轴上方的概率为![]() .
.
【解析】
(1)用列表法或树状图法求出所有可能即可;
(2)根据表格或树状图得出点在x轴上方的情况数,再结合概率公式可求出概率.
解:(1)列表如下:
-2 | -1 | 1 | 2 | |
-2 | (-1,-2) | (1,-2) | (2,-2) | |
-1 | (-2,-1) | (1,-1) | (2,-1) | |
1 | (-2,1) | (-1,1) | (2,1) | |
2 | (-2,2) | (-1,2) | (1,2) |
或画树图如下:
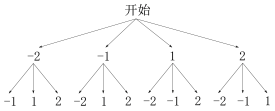
故所有可能的点的坐标为(-1,-2),(1,-2),(2,-2),(-2,-1),(1,-1),(2,-1),(-2,1),(-1,1),(2,1),(-2,2),(-1,2),(1,2);
∴点在x轴上方的概率=![]() =
=![]() .
.

练习册系列答案
相关题目