Question

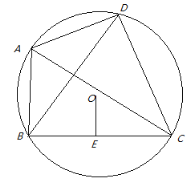
【题目】如图，已知：四边形ABCD内接于⊙O，对角线AC⊥BD，⊙O的半径为6cm，AD=4cm，OE⊥BC，垂足为E.则弦BC的长为____________．

Answer 1

【答案】8cm

【解析】

连接CO并延长交⊙O于点P，连接PB，PA，则CP为⊙O直径，即∠PAC=90°，由已知AC⊥BD，可得AP∥BD，即∠PAB=∠ABD，即AD=AB=4cm，即OE=2cm，再根据在Rt△OEC中利用勾股定理求得CE的长，CB的长为CE2倍．

解：如图，连接CO并延长交⊙O于点P，连接PB，PA，

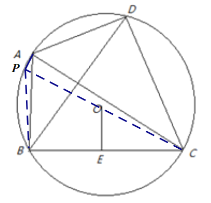
∵CP是⊙O的直径，

∴∠CBP=∠CAP=90°，

∴PA⊥AC，

∵AC⊥BD，

∴AP∥BD，

∴∠BAP=∠ABD，

∴ ，

∴PB=AD=4cm，

∵OE⊥BC，

∴，

∵⊙O的半径为6cm，

∴，

∴，

∴cm，

故答案为：cm．