Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，分别以ACBC为底边，向△ABC外部作等腰△ADC和△CEB，点M为AB中点，连接MDME分别与ACBC交于点F和点G．

求证四边形MFCG是矩形．

Answer 1

【答案】详见解析

【解析】

根据Rt△ABC，得出点M在线段AC的垂直平分线上．然后在等腰△ADC中，AC为底边，得到MD垂直平分AC．即可解答

证明：连接CM，

∵Rt△ABC中，∠ACB＝90°，M为AB中点，

∴ CM＝AM＝BM＝ AB．

∴点M在线段AC的垂直平分线上．

∵在等腰△ADC中，AC为底边，

∴AD＝CD．

∴点D在线段AC的垂直平分线上．

∴MD垂直平分AC．

∴∠MFC＝90°．

同理：∠MGC＝90°．

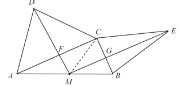∴四边形MFCG是矩形．