题目内容
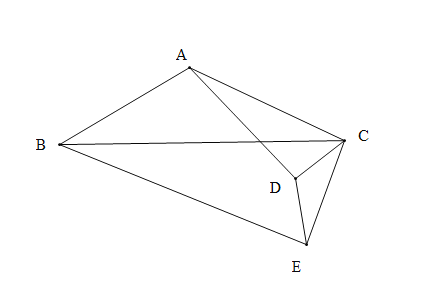
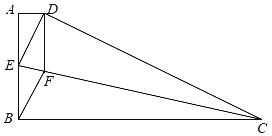
【题目】如图,四边形ABCD中,AD//BC,∠A=90°,CD=CB,过点C作∠DCB的平分线CE交AB于点E,连接DE,过点D作DF//AB,且交CE于F点,连接BF.
(1)求证:四边形DEBF是菱形;
(2)若AB=5,BC=13,求tan∠AED的值.
【答案】(1)见解析;(2)tan∠AED=![]() .
.
【解析】
(1)证明△CDE≌△CBE,根据全等三角形的性质得到ED=EB,∠DEC=∠BEC,根据平行线的性质、等腰三角形的判定定理得到DE=DF,根据菱形的判定定理证明;
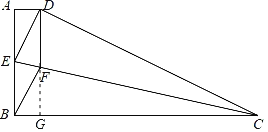
(2)根据矩形的性质得到∠BGD=90°,DG=AB=5,AD=BG,根据勾股定理求出GC,求出AD,根据勾股定理列方程求出AE,根据正切的定义计算,得到答案.
解:(1)证明:∵CE平分∠DCB,
∴∠DCE=∠BCE,
在△CDE和△CBE中,
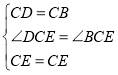
∴△CDE≌△CBE(SAS),
∴ED=EB,∠DEC=∠BEC,
∵DF//AB,
∴∠DFE=∠BEC,
∴∠DFE=∠DEC,
∴DE=DF,
∴DF=BE,又DF//AB,DE=DF,
∴四边形DEBF为菱形;
(2)∵AD//BC,AB//DF,
∴四边形ABGD为平行四边形,
∵∠A=90°,
∴四边形ABGD为矩形,
∴∠BGD=90°,DG=AB=5,AD=BG,
在Rt△DGC中,GC=![]() =12,
=12,
∴AD=BG=BC﹣GC=13﹣12=1,
设AE=x,则DE=BE=5﹣x,
在Rt△ADE中,DE2=AE2+AD2,即(5﹣x)2=x2+12,
解得,x=![]() ,
,
∴tan∠AED=![]() =
=![]() .
.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目