题目内容
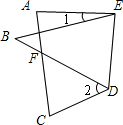
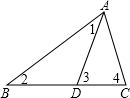
如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，则∠DAC=（ ）
| A．78° | B．39° | C．24° | D．48° |
假设∠1=∠2=x°．
∵∠3是三角形ABD的外角，
∴∠3=∠1+∠2=2x°，
又∵∠3=∠4，
∴∠4=2x°．
根据△ABC中内角和是180°，得到方程x°+2x°+63°=180°，
解方程得x=39．
根据△ADC中内角和180°，得到∠DAC=180°-2x°-2x°=24°．
故选C．
∵∠3是三角形ABD的外角，
∴∠3=∠1+∠2=2x°，
又∵∠3=∠4，
∴∠4=2x°．
根据△ABC中内角和是180°，得到方程x°+2x°+63°=180°，
解方程得x=39．
根据△ADC中内角和180°，得到∠DAC=180°-2x°-2x°=24°．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
