题目内容
平面内有n条直线（n≥2），这n条直线两两相交，最多可以得到a个交点，最少可以得到b个交点，则a+b的值是（ ）
| A．n（n-1） | B．n2-n+1 | C．
| D．
|
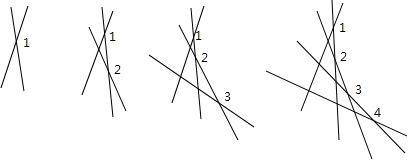
如图：2条直线相交有1个交点；
3条直线相交有1+2个交点；
4条直线相交有1+2+3个交点；
5条直线相交有1+2+3+4个交点；
6条直线相交有1+2+3+4+5个交点；
…
n条直线相交有1+2+3+4+5+…+（n-1）=
个交点．
所以a=
，而b=1，
∴a+b=
．
故选D．
3条直线相交有1+2个交点；
4条直线相交有1+2+3个交点；
5条直线相交有1+2+3+4个交点；
6条直线相交有1+2+3+4+5个交点；
…
n条直线相交有1+2+3+4+5+…+（n-1）=
| n(n-1) |
| 2 |
所以a=
| n(n-1) |
| 2 |
∴a+b=
| n2-n+2 |
| 2 |
故选D．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
