Question

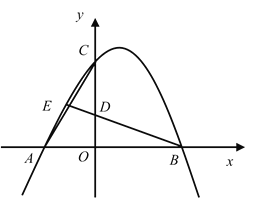
【题目】如图，已知抛物线经过点，，，点为中点，连接、，并延长交于点．

（1）求抛物线的表达式；

（2）若抛物线与抛物线关于轴对称，在抛物线位于第二象限的部分上取一点，过点作轴，垂足为点，是否存在这样的点，使得与相似？若存在，请求出点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）；（2）存在，，

【解析】

（1）设抛物线的解析式为y=ax2＋bx＋c，将A（1，0），B（2，0），C（0，2）代入抛物线的解析式即可解答；

（2）求出抛物线w2的解析式y=x2x＋2，可知点D坐标，证明△AOC∽△DOB，可证出BD⊥AC，则，设F（m,0），，m＜0，若△QFO与△CDE相似，可分两种情况考虑，①是△QFO∽△DEC时，②是△QFO∽△CED时，列出相似比即可求出m的值．

解：（1）设抛物线的解析式为y=ax2＋bx＋c，将A（1，0），B（2，0），C（0，2）代入抛物线的解析式得：，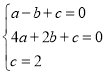
解得：a=1，b=1，c=2，
∴抛物线w1的表达式为y=x2＋x＋2；
（2）∵抛物线w1与抛物线w2关于y轴对称，
∴抛物线w2的解析式y=x2x＋2，
∵点D为OC中点，C（0，2），
∴D（0，1），
∵A（1，0），B（2，0），
∴，

∵∠AOC=∠BOD=90°，

∴△AOC∽△DOB，

∴∠ACO=∠DBO，

∴BD⊥AC，

∴，

设F（m,0），，m＜0，若△QFO与△CDE相似，可分两种情况考虑：

①△QFO∽△DEC时，

∴，

解得：（舍去）

∴，

②△QFO∽△CED时，

，

∴，

解得：（舍去）

∴F（-1,0）；

综上所述： ，