Question

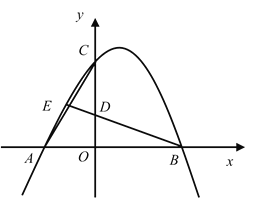
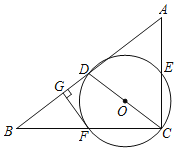
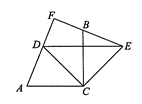
【题目】如图，∠ACB=90°，AC=BC，CD平分∠ACB，点D，E关于CB对称，连接EB并延长，与AD的延长线交于点F，连接DE，CE．对于以下结论：

①DE垂直平分CB；②AD=BE；③∠F不一定是直角；④EF2＋DF2=2CD2．

其中正确的是(　　)

A.①④B.②③C.①③D.②④

Answer 1

【答案】D

【解析】

根据点D，E关于CB对称，可得CB垂直平分DE，即可判断①错误；根据CB垂直平分DE，连接BD，可得BD=BE，证明△ACD≌△BCD，可得AD=BD，即可判断②；结合①②证明△ACD≌△BCD≌△BCE，可得∠CAD=∠CEB=(180°-45°)=67.5°，∠FED=67.5°-45°=22.5°，进而证明角F的度数，即可判断③；在Rt△FDE中，根据勾股定理，得EF2+DF2=DE2，根据∠DCE=90°，CD=CE，即可判断④．

①∵点D、E关于CB对称，
∴CB垂直平分DE，
所以①错误；
②连接BD，如图，

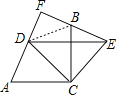
∵CB垂直平分DE，
∴BD=BE，
∵∠ACB=90°，CD平分∠ACB，
∴∠ACD=∠BCD=45°，
在△ACD和△BCD中，

，
∴△ACD≌△BCD(SAS)，
∴AD=BD，
∴AD=BE，
所以②正确；
③∵CB垂直平分DE，
∴BD=BE，CD=CE，
在△BCD和△BCE中，

，
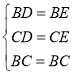∴△BCD≌△BCE(SSS)，
∴△ACD≌△BCD≌△BCE，
∴∠ACD=∠DCB=∠ECB=45°，
∴CA=CD=CB=CE，
∴∠CAD=∠CEB=(180°-45°)=67.5°，

∵∠CED=∠CDE=(180°-∠DCB-∠ECB) =45°，
∴∠FED=67.5°-45°=22.5°，
∵∠CDE=∠ACD=45°，

∴DE∥AC，
∴∠FDE=∠A=67.5°，
∴∠F=180°-∠FDE-∠FED=90°，
所以③错误；
④在Rt△FDE中，根据勾股定理，得：
EF2+DF2=DE2，
∵∠DCE=∠DCB+∠ECB=90°，CD=CE，
∴DE2=CD2+CE2=2CD2，
∴EF2+DF2=2CD2，
所以④正确．
综上所述：正确的是②④．
故选：D．