题目内容
【题目】完成下面推理过程:
已知:如图,已知∠1 =∠2,∠B =∠C,
求证:AB∥CD.
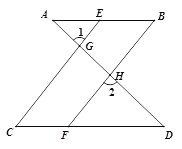
证明∵∠1 =∠2(已知),
且∠1 =∠CGD( ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
【答案】对顶角相等. 同位角相等,两直线平行. ∠BFD, 两直线平行,同位角相等, ∠BFD, 内位角相等,两直线平行.
【解析】试题分析:根据对顶角相等,易得∠1=∠CGD,通过等量代换得到∠2=∠CGD,而其互为同位角,据此可得CE和BF的位置关系;再根据平行线的性质,结合∠BFD和∠C为同位角,∠B=∠C,可得∠B和∠BFD的关系,而∠B和∠BFD互为内错角,至此问题不难解决.
试题解析:∵∠1=∠2(已知),
且∠1=∠CGD(对顶角相等),
∴∠2=∠CGD(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠BFD=∠C(两直线平行,同位角相等),
又∵∠B=∠C(已知),
∴∠BFD=∠B(等量代换).
∴AB∥CD(内错角相等,两直线平行).
故答案为:对顶角相等. 同位角相等,两直线平行. ∠BFD, 两直线平行,同位角相等, ∠BFD, 内位角相等,两直线平行.

练习册系列答案
相关题目