题目内容
【题目】已知:如图,△ABC中,∠ABC=45°,AD为△ABC的高,点E在边AC上,BE与AD交于点F,且DF=DC.
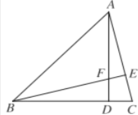
求证;(1)BF=AC;
(2)BE![]() AC.
AC.
【答案】(1)证明见详解;(2)证明见详解.
【解析】
(1)由∠ABC=45°,AD为△ABC的高,得到△ABD是等腰直角三角形,则AD=BD,然后证明△ACD≌△BFD,即可得到BF=AC;
(2)由(1)知∠FBD=∠CAD,由对顶角相等,则∠BFD=∠AFE,即可得到∠BDF=∠AEF,即可得到BE⊥AC.
证明:(1)∵AD为△ABC的高,
∴∠ADB=∠ADC=90°,
∵∠ABC=45°,
∴△ABD是等腰直角三角形,
∴BD=AD,
∵DF=DC,
∴△BDF≌△AEF(SAS),
∴BF=AC;
(2)由(1)知△BDF≌△AEF,
∴∠FBD=∠CAD,
∵∠BFD=∠AFE,
∵∠BDF+∠FBD+∠BFD=180°,∠AEF+∠CAD+∠AFE=180°,
∴∠BDF=∠AEF=90°,
∴BE⊥AC.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目





