题目内容
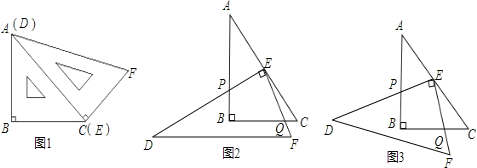
【题目】已知,如图, 在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结
,P是边BC上的一动点,过点P作PE⊥AB,垂足为E,延长PE至点Q,使PQ=PC, 联结![]() 交边AB于点
交边AB于点![]() .
.
(1)求AD的长;
(2)设![]() ,
,![]() 的面积为y, 求y关于x的函数解析式,并写出定义域;
的面积为y, 求y关于x的函数解析式,并写出定义域;
(3)过点C作![]() , 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,
, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时,![]() 为等边三角形?请指出点P的位置并加以证明.
为等边三角形?请指出点P的位置并加以证明.

【答案】(1)证明见解析;(2)![]() ,定义域为
,定义域为![]() .(3)点
.(3)点![]() 是边
是边![]() 的中点,证明见解析.
的中点,证明见解析.
【解析】
(1)根据直角三角形的性质和三角形的内角和定理,进行计算,即可得到答案;
(2)作![]() ,垂足为点
,垂足为点![]() .根据勾股定理进行计算,即可得到答案;
.根据勾股定理进行计算,即可得到答案;
(3)根据等腰三角形的性质和判定即可得到答案.
解:(1)在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]()
∵![]() ∴
∴![]() .
.
∵![]() ∴
∴![]() 90° ∴
90° ∴![]() 90°.
90°.
∵![]() =90°,∴
=90°,∴![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
(2)作![]() ,垂足为点
,垂足为点![]() .
.
∵![]() 90°,∴
90°,∴![]() =90°,∴
=90°,∴![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
∴![]() ,即
,即![]()
定义域为![]() .
.
(3)点![]() 是边
是边![]() 的中点.
的中点.
证明:∵![]() ,点
,点![]() 是边
是边![]() 的中点.
的中点.
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() 是等边三角形
是等边三角形
∴![]()
∵![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() 是等边三角形
是等边三角形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目