题目内容
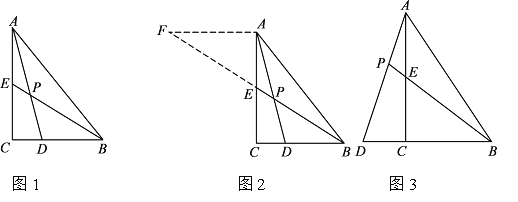
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,AB=4,点
,AB=4,点![]() 是边
是边![]() 上动点(点
上动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() .
.

(1)求![]() 的大小;
的大小;
(2)若把![]() 沿着直线
沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
① 如图2,当点![]() 落在斜边
落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,![]() 与
与![]() 相交于点
相交于点![]() ,如果
,如果![]() ,写出
,写出![]() 与
与![]() 的函数关系式以及定义域.
的函数关系式以及定义域.
【答案】(1) ![]() ;(2) ①x=1,②
;(2) ①x=1,② ![]() ,定义域
,定义域![]()
【解析】
(1)根据正弦的定义求出∠B=30°,根据平行线的性质解答;
(2)根据翻转变换的性质,等边三角形的判定定理得到△AQP为等边三角形,根据等边三角形的性质得到AQ=QP,证明AQ=QC,计算即可;
(3)作QG⊥AB于G,RH⊥AB于H,根据正弦的定义用x表示出QG,证明RE=RB,根据等腰三角形的性质得到EH= ![]() y,根据正切的定义计算即可.
y,根据正切的定义计算即可.
解:(1) 在Rt△ABC中,
∵ ![]() ,AB=4,
,AB=4,
![]()
∴![]()
∵![]()
∴![]()
(2) ① 如图2,当点![]() 落在斜边
落在斜边![]() 上时;
上时;
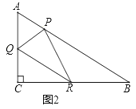
由翻折得![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
![]() 是等边三角形
是等边三角形
![]()
即x=1.
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,
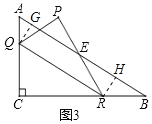
作QG⊥AB于G,
∵QR∥AB,
∴QG=RH,
在Rt△AQG中,QG=AQ×sinA![]()
由翻折的性质可知,∠PRP=∠CRQ=30°,
∵QR∥AB,
∴∠REB=∠PRQ,
∴∠REB=∠B,
∴RE=RB,
∵RH⊥AB,
![]()
在Rt△ERH中,![]()
∴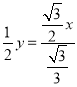
整理得,y=3x,
则y与x的函数关系式为y=3x(0<x<1).

练习册系列答案
相关题目