Question

【题目】已知，点是线段所在平面内任意一点，分别以、为边，在同侧作等边和等边，联结、交于点．

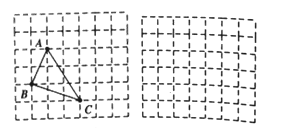
(1)如图1，当点在线段上移动时，线段与的数量关系是:________；

(2)如图2，当点在直线外，且，仍分别以、为边，在 同侧作等边和等边，联结、交于点．(1)的结论是否还存在？若成立，请证明；若不成立，请说明理由．此时是否随的大小发生变化？若变化，写出变化规律，若不变，请求出的度数；

(3)如图3，在(2)的条件下，联结，求证： 平分．

Answer 1

【答案】(1) ；(2)成立，证明见解析， ；(3) 证明见解析.

【解析】试题分析：（1）直接写出答案即可．

（2）证明ΔACD≌ΔECB，得到∠CEB=∠CAD，此为解题的关键性结论；借助内角和定理即可解决问题．

（3）过点C分别作CM⊥AD于M，CN⊥EB于N，由ΔACD≌ΔECB，得到CM=CN，从而得到结论．

试题解析：解：（1）∵△ACE、△CBD均为等边三角形，∴AC=EC，CD=CB，∠ACE=∠BCD，∴∠ACD=∠ECB；

在△ACD与△ECB中，∵AC=EC，∠ACD=∠ECB，CD=CB，∴△ACD≌△ECB（SAS），∴AD=BE，故答案为：AD=BE．

（2）AD=BE成立，∠APE不随着∠ACB的大小发生变化，始终是60°．

证明如下：

∵ΔACE和ΔBCD是等边三角形，∴AC=EC，CD=CB，∠ACE=∠BCD，∴∠BCE=∠ACD，

在ΔACD和ΔECB中，∵AC=EC，∠BCE=∠ACD，CD=CB，∴ΔACD≌ΔECB，∴AD=BE．

∵ΔACD≌ΔECB，∴∠CAD=∠CEB，∵∠APB=∠PAE+∠PEA，∴∠APB=∠CAE+∠CEA=120°，∴∠APE=60°；

（3）过点C分别作CM⊥AD于M，CN⊥EB于N，∵ΔACD≌ΔECB，∴CM=CN，∴CP平分∠DPE．