题目内容
【题目】若等腰三角形一边上的高等于腰长的一半,则等腰三角形的底角为_______.
【答案】75°或15°或30°
【解析】
分情况讨论:等腰三角形腰上的高在内部、腰上的高在外部和底边上高等于腰长的一半;分别作出图形,根据含30度角的直角三角形的性质,结合三角形内角和定理及外角的性质求解即可.
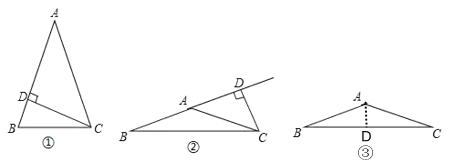
解:如图①,∵CD⊥AB,
∴∠ADC=90°,
∵CD=![]() AC,
AC,
∴∠A=30°,
∵AB=AC,
∴∠B=∠ACB=![]() =75°;
=75°;
如图②,∵CD⊥AB,
∴∠ADC=90°,
∵CD=![]() AC,
AC,
∴∠CAD=30°,
∵AB=AC,
∴∠B=∠ACB,
∴∠DAC=∠B+∠ACB=2∠B=30°,
∴∠B=∠ACB=15°;
如图③,∵AD⊥BC,
∴∠ADB=90°,
∵AD=![]() AB,
AB,
∴∠B=30°;
综上,三角形的底角为:75°或15°或30°,
故答案为:75°或15°或30°.

练习册系列答案
相关题目