题目内容
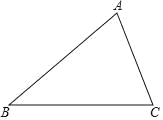
【题目】已知∠AOB=90°,OM是∠AOB的平分线,按以下要求解答问题:
(1)如图1,将三角板的直角顶点P在射线OM上移动,两直角边分别与OA,OB交于点C,D.
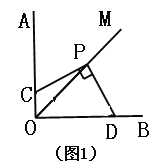
①比较大小:PC______PD. (选择“>”或“<”或“=”填空);
②证明①中的结论.
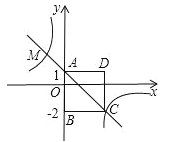
(2)将三角板的直角顶点P在射线OM上移动,一直角边与边OA交于点C,且OC=1,另一直角边与直线OB,直线OA分别交于点D,E,当以P,C,E为顶点的三角形与△OCD相似时,试求![]() 的长.(提示:请先在备用图中画出相应的图形,再求
的长.(提示:请先在备用图中画出相应的图形,再求![]() 的长).
的长).

【答案】(1)①PC=PD;②证明见解析;(2)OP=1或OP=![]() .
.
【解析】
试题(1)①PC=PD;②过P作PH⊥OA,PN⊥OB,再证△PCH≌△PDN,即可;
(2)分两种情况进行讨论:①若PD与边OB相交;②PD与边OB的反向延长线相交.
试题解析:(1)①PC=PD;
②过P作PH⊥OA,PN⊥OB,垂足分别为H,N,得∠HPN=90°,
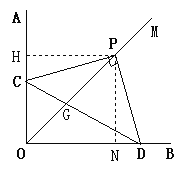
∴∠HPC+∠CPN=90°
∵∠CPN+∠NPD=90°,
∴∠HPC=∠NPD,
∵OM是∠AOB的平分线,
∴PH=PN.
又∵∠PHC=∠PND=90°
∴△PCH≌△PDN,
∴PC=PD;
(2)①若PD与边OB相交
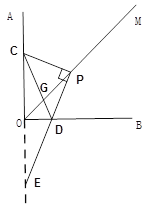
∵∠PCE>∠DCO,∠CPE=∠DOC=90°
∴由△PCE与△OCD相似可得∠PEC=∠DCO
∴DE=CD,而DO⊥OC,
∴OE="OC=1"
∴OP为Rt△CPE斜边上的中线
∴OP=![]() EC="OC=1" ;
EC="OC=1" ;
②若PD与边OB的反向延长线相交, 过P作PH⊥OA,PN⊥OB,垂足分别为H,N, 则PH=PN
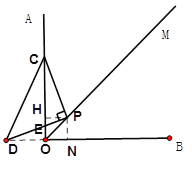
∵△PCE与△DCO相似,且∠PEC>∠OCD,∠CPE=∠DOC=90°
∴∠PCE=∠OCD
又∵∠PCO+∠PEC=90°,∠PDO +∠OED =90°,
且∠PEC=∠OED,∴∠PDO=∠PCO.
而PH=PN,∴Rt△PHC≌Rt△PND(A.A.S).
∴HC=ND,PC=PD, ∴∠PCD= ∠PDC =45°,
∴∠PCO=∠DCO=∠PDO =22.5°
又∠BOM=∠ODP+∠OPD=45°,
∴∠ODP=∠OPD=22.5°
∴OP=OD,
设OP=x,则HC=OC-OH=![]() ,
,
而DN=DO+ON=OP+ON=![]() , ∴
, ∴![]() ,
,
∴![]() ,即OP=
,即OP=![]() ,
,
综上所述,满足条件的OP=1或OP=![]() .
.

 小学生10分钟口算测试100分系列答案
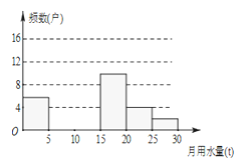
小学生10分钟口算测试100分系列答案【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
60≤x<70 | 2 | 0.04 |
请解答以下问题:
(1)求出吗、M,n的值,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?