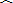题目内容
如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过△ABC的内切圆圆心O，且点E在半圆弧上．①若正方形的顶点F也在半圆弧上，则半圆的半径与正方形边长的比是______；②若半圆的直径AB=21，△ABC的内切圆半径r=4，则正方形DEFG的面积为______．
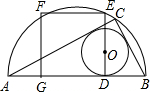
①如图，根据圆和正方形的对称性可知：GH=
DG=
GF，
H为半圆的圆心，不妨设GH=a，则GF=2a，
在直角三角形FGH中，由勾股定理可得HF=
a．由此可得，半圆的半径为
a，正方形边长为2a，
所以半圆的半径与正方形边长的比是
a：2a=
：2；
②连接OI、OJ，可得OICJ是正方形，且边长是4，
设BD=x，AD=y，则BD=BI=x，AD=AJ=y，
在直角三角形ABC中，由勾股定理得（x+4）2+（y+4）2=（x+y）2；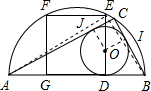
∴8（x+y）+32=2xy，
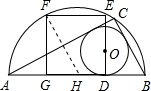
在直角三角形AEB中，可以证得△ADE∽△EBD∽△ABE，
于是得到ED2=AD•BD，即102=x•y②．
∴正方形DEFG的面积为：100，
故答案为：①
：2，②100．
| 1 |
| 2 |
| 1 |
| 2 |
H为半圆的圆心，不妨设GH=a，则GF=2a，
在直角三角形FGH中，由勾股定理可得HF=
| 5 |
| 5 |
所以半圆的半径与正方形边长的比是
| 5 |
| 5 |
②连接OI、OJ，可得OICJ是正方形，且边长是4，
设BD=x，AD=y，则BD=BI=x，AD=AJ=y，
在直角三角形ABC中，由勾股定理得（x+4）2+（y+4）2=（x+y）2；
∴8（x+y）+32=2xy，
在直角三角形AEB中，可以证得△ADE∽△EBD∽△ABE，
于是得到ED2=AD•BD，即102=x•y②．
∴正方形DEFG的面积为：100，
故答案为：①
| 5 |
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
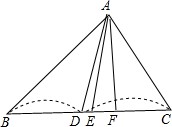的线段在△ABC中有几条？
