Question

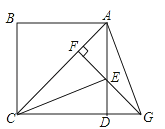
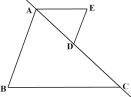
【题目】如图1，AB，BC被直线AC所截，点D是线段AC上的点，过点D作DE//AB，连接AE，∠B=∠E=70°.

（1）请说明AE//BC的理由.

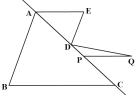
（2）将线段AE沿着直线AC平移得到线段PQ，连接DQ.

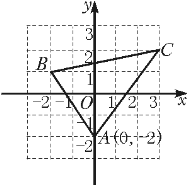
①如图2，当DE⊥DQ时，求∠Q的度数；

②在整个运动中，当∠Q=2∠EDQ时，则∠Q= .

Answer 1

【答案】（1）详见解析；（2）①20°；②

【解析】

（1）由DE//AB，可得∠BAE+∠E=180°，从而可证∠BAE+∠B=180°，根据从旁内角互补，两直线平行可证AB//DE；

(2)①过D点作DF//AE，由平行线的性质可得∠EDF=70°，由DE⊥DQ，可得∠FDQ=20°，进而可的求出∠Q=20°；②如图，作DF//AE，根据平行线的性质解答即可.

（1）证明：∵DE//AB，

∴∠BAE+∠E=180°.

又∵∠B=∠E，

∴∠BAE+∠B=180°，

∴AB//DE；

(2)①过D点作DF//AE，

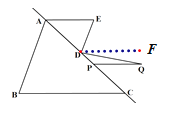
∵PQ//AE ，

∴DF//PQ，

∵∠E=70°，

∴∠EDF=70°.

∵DE⊥DQ，

∴∠EDQ=90°，

∴∠FDQ=90°-70°=20°，

∴∠Q=∠FDQ=20°；

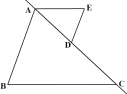
②如图，作DF//AE，

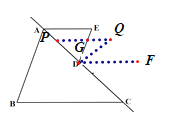
∵PQ//AE ，

∴DF//PQ，

∴∠Q=∠QDF，∠E=∠EDF=70°，

∴∠EDQ+∠Q=70°，

∵∠Q=2∠EDQ，

∴∠Q+∠Q=70°，

∴∠Q=（）°.