Question

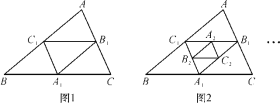
【题目】如图，在图1中，A1，B1，C1分别是△ABC的边BC，CA，AB的中点，在图2中，A2，B2，C2分别是△A1B1C1的边B1C1，C1A1，A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有___个．

Answer 1

【答案】3n

【解析】

在图１中，有3个平行四边形；在图2中，有6个平行四边形；.观察发现规律即可完成解答．.

解：在图1中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，

∴A1C1//AC,A1B1∥AB,BC //B1C , A1C1=AC,A1B1=AB,BC =B1C，

∴四边形A1B1AC1、A1B1C1B、A1C1B1C是平行四边形，共有3个；

同理，第2个图形有6个，第3个图形有9个，以此类推可得，第n个图形有3n个．

故答案为3n．