题目内容
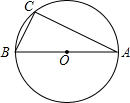
如图，△ABC内接于⊙O，BC=a，CA=b，∠A-∠B=90°，则⊙O的半径为______．
过点B作圆的直径BE交于圆于点E，连接CE，
∴∠ECB=90°，
∴∠E+∠EBC=90°，
∴∠E+∠A=180°，
∵∠A-∠ABC=90°，
∴∠CBA=∠CBE，
弧AC=弧CE，CE=CA=b，
由勾股定理得，BE=
，
∴⊙O的半径=
．
∴∠ECB=90°，
∴∠E+∠EBC=90°，
∴∠E+∠A=180°，
∵∠A-∠ABC=90°，
∴∠CBA=∠CBE，
弧AC=弧CE，CE=CA=b，
由勾股定理得，BE=
| a2+b2 |
∴⊙O的半径=
| ||
| 2 |
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
