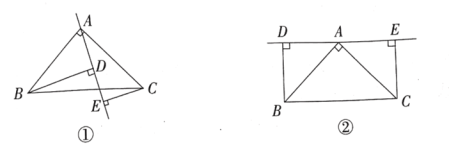Question

【题目】（1）如图1，在四边形中，，，、分别是边、上的点，若，可求得、、之间的数量关系为______．（只思考解题思路，完成填空即可，不必书写证明过程）

（2）如图2，在四边形中，，，、分别是边、延长线上的点，若，判断、、之间的数量关系还成立吗，若成立，请完成证明，若不成立，请说明理由．（可借鉴第（1）问的解题经验）

Answer 1

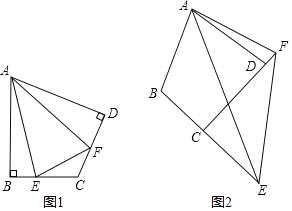
【答案】（1）EF=BE+DF；（2）不成立，证明见解析．

【解析】

（1）延长CB至M，使BM=DF，证明△ABM≌△ADF，再证明△EAH≌△EAF，可得出结论；
（2）在BE上截取BG，使BG=DF，连接AG．证明△ABG≌△ADF和△AEG≌△AEF，即可得出EF=BE-FD．

（1）EF=BE+DF；
如图，延长CB至M，使BM=DF，

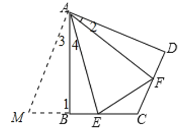
∵∠ABC =∠D =90°，
∴∠1=∠D，
在△ABM与△ADF中，

，
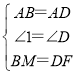∴△ABM≌△ADF（SAS）．
∴AF=AM，∠2=∠3，

∵，

∴∠2+∠4=∠BAD=∠EAF，

∴∠3+∠4=∠EAF，即∠MAE=∠EAF．
在△AME与△AFE中，

，

∴△AME≌△AFE（SAS）．
∴EF=ME，即EF=BE+BM．
∴EF=BE+DF．

（2）不成立，应该是EF=BE-FD．
证明：如图2，在BE上截取BG，使BG=DF，连接AG．

∵∠B+∠ADC=180°，∠ADF+∠ADC=180°，
∴∠B=∠ADF．
∵在△ABG与△ADF中，

，
∴△ABG≌△ADF（SAS）．
∴∠BAG=∠DAF，AG=AF．
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=∠BAD，

∴∠GAE=∠EAF．

∵在△AEG与△AEF中，，
∴△AEG≌△AEF（SAS）．
∴EG=EF，
∵EG=BE-BG，
∴EF=BE-FD．