题目内容
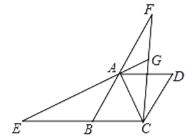
【题目】有一个测量弹跳力的体育器材,如图所示,竖杆![]() 的长度分别为200厘米和300厘米,
的长度分别为200厘米和300厘米,![]() 厘米.现有一人站在斜杆
厘米.现有一人站在斜杆![]() 下方的点
下方的点![]() 处,直立、单手上举时中指指尖(点
处,直立、单手上举时中指指尖(点![]() )到地面的高度
)到地面的高度![]() 厘米,屈膝尽力跳起时,中指指尖刚好触到斜杆的点
厘米,屈膝尽力跳起时,中指指尖刚好触到斜杆的点![]() 处,此时,就将
处,此时,就将![]() 与
与![]() 的差值
的差值![]() (厘米)作为此人此次的弹跳成绩,设
(厘米)作为此人此次的弹跳成绩,设![]() 厘米.
厘米.
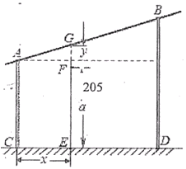
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)若他弹跳时的位置为![]() ,求该人的弹跳成绩.
,求该人的弹跳成绩.
【答案】(1)y=![]() ;(2)45cm
;(2)45cm
【解析】
(1)根据题意,构造直角△AGK与△AHB,由△AGK∽△AHB,得:GK∶BH=AK∶AH;
(2)将![]() 的值代入函数关系式从而得到结果.
的值代入函数关系式从而得到结果.
解:过A作AH⊥BD,交BD于H,AH交GE于K.
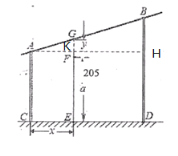
(1)由已知可得GE∥BD,所以△AGK∽△AHB,得:GK∶BH=AK∶AH
即:![]() ,
,
整理得:y=![]()
(2)当![]() 时,y=
时,y=![]() (cm)
(cm)
所以该人的弹跳成绩45cm.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
【题目】某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元。根据市场需求,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件利润减少2元,设每天安排![]() 人生产乙产品。
人生产乙产品。
(1)根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | — | — | 15 |
乙 |
|
| — |
(2)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等,已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润![]() (元)的最大值及相应的
(元)的最大值及相应的![]() 值。
值。