��Ŀ����
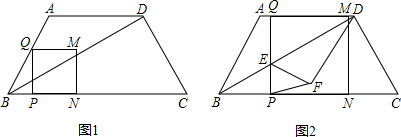
��ͼ1������ABCD�У�AD��BC��AB=AD=DC=5��BC=11��һ������P�ӵ�B��������ÿ��1����λ���ȵ��ٶ����߶�BC�����˶�������P��PQ��BC�������߶�BA-AD�ڵ�Q����PQΪ��������������PQMN����N������BC�ϣ���Q�㵽��D��ʱ���˶����������P���˶�ʱ��Ϊt�루t��0����
��1����������PQMN�ı�MNǡ�þ�����Dʱ�����˶�ʱ��t��ֵ��
��2���������˶������У���������PQMN���BCD���غϲ������ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��
��3����ͼ2������Q���߶�AD���˶�ʱ���߶�PQ��Խ���BD���ڵ�E������DEQ��BD���ۣ��õ���DEF������PF���Ƿ����������t��ʹ��PEF�ǵ��������Σ������ڣ������Ӧ��t��ֵ���������ڣ���˵�����ɣ�
��1����������PQMN�ı�MNǡ�þ�����Dʱ�����˶�ʱ��t��ֵ��
��2���������˶������У���������PQMN���BCD���غϲ������ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��
��3����ͼ2������Q���߶�AD���˶�ʱ���߶�PQ��Խ���BD���ڵ�E������DEQ��BD���ۣ��õ���DEF������PF���Ƿ����������t��ʹ��PEF�ǵ��������Σ������ڣ������Ӧ��t��ֵ���������ڣ���˵�����ɣ�

��������1����AG��BC��DH��BC������ֱ�ΪG��H�����Եó��ı���AGHDΪ���Σ����ݾ��ε����ʼ�����������Եó���ABG�ա�DCH���������BG=CH��ֵ�����ɹ��ɶ����Ϳ������AG=DH��ֵ���Ϳ������BP��ֵ���������������t��ֵ��
��2��������ֶκ����ķ������������������0��t��3����3��t��4��4��t��7��7��t��8ʱ���������ε������ʽ�������ε������ʽ�Ϳ������S��ֵ��
��3�����������������EF=EQ=PQ-EP=4-
t����Ϊ���������EF=EPʱ�������tֵ����FE=FPʱ����FR��EP������ΪR���������tֵ����PE=PFʱ����PS��EF������ΪS���������tֵ��
��2��������ֶκ����ķ������������������0��t��3����3��t��4��4��t��7��7��t��8ʱ���������ε������ʽ�������ε������ʽ�Ϳ������S��ֵ��
��3�����������������EF=EQ=PQ-EP=4-
| 1 |
| 2 |
����⣺��1����ͼ2����AG��BC��DH��BC������ֱ�ΪG��H��
���ı���AGHDΪ���Σ�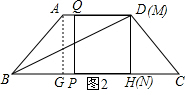
������ABCD��AB=AD=DC=5��
���ABG�ա�DCH��
��BG=
��BC-AD��=3��AG=4��
�൱������PQMN�ı�MNǡ�þ�����Dʱ����M���D�غϣ���ʱMQ=4��
��GP=AQ=AD-DQ=1��BP=BG+GP=4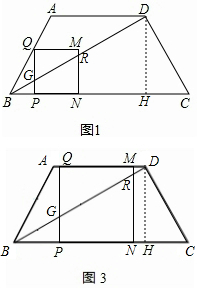 ��
��
��t=4����4��ʱ��������PQMN�ı�MNǡ�þ�����D��
��2����ͼ1����0��t��3ʱ��BP=t��
��tan��DBC=
��tan��C=tan��ABC=
��
��GP=
t��PQ=
t��BN=t+
t=
t��
��NR=
t��
��S=
=
t2��
��ͼ3����3��t��4ʱ��BP=t��
��GP=
t��PQ=4��BN=t+4��
��NR=
t+2��
��S=
=2t+4��
��ͼ4����4��t��7ʱ��BP=t��
��GP=
t��PQ=4��PH=8-t��BN=t+4��HN=t+4-8=t-4��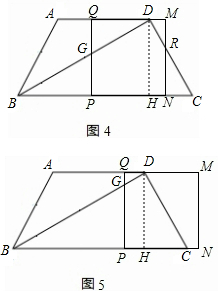
��CN=3-��t-4��=7-t��
��NR=
��
��S=
+
=-
t2+
t-
��
��ͼ5����7��t��8ʱ��BP=t��
��GP=
t��PQ=4��PH=8-t��
��S=
+
=-
t2+22��
��S=
��
��3���ߡ�PEF+��QEF=180��=��QDF+��QEF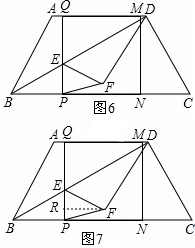 ��
��
���PEF=��QDF=2��ADB=��ABC��
��cos��ABC=cos��PEF=
��
�ɣ�1����֪EP=
BP=
t��
��EF=EQ=PQ-EP=4-
t��
����ͼ6����EF=EPʱ��4-
t=
t��
��t=4��
����ͼ7����FE=FPʱ����FR��EP������ΪR��
��ER=
EP=
EF��
��
•
t=
(4-
t)��
��t=
��
 ����ͼ8����PE=PFʱ����PS��EF������ΪS��
����ͼ8����PE=PFʱ����PS��EF������ΪS��
��ES=
EF=
PE��
��
��4-
t��=
•
t��
��t=
��
�൱t=4��
��
ʱ����PEF�ǵ��������Σ�
���ı���AGHDΪ���Σ�

������ABCD��AB=AD=DC=5��
���ABG�ա�DCH��
��BG=
| 1 |
| 2 |
�൱������PQMN�ı�MNǡ�þ�����Dʱ����M���D�غϣ���ʱMQ=4��
��GP=AQ=AD-DQ=1��BP=BG+GP=4
 ��
����t=4����4��ʱ��������PQMN�ı�MNǡ�þ�����D��
��2����ͼ1����0��t��3ʱ��BP=t��
��tan��DBC=
| 1 |
| 2 |
| 4 |
| 3 |
��GP=
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
��NR=
| 7 |
| 6 |
��S=
(
| ||||||
| 2 |
| 10 |
| 9 |
��ͼ3����3��t��4ʱ��BP=t��
��GP=
| 1 |
| 2 |
��NR=
| 1 |
| 2 |
��S=
(
| ||||
| 2 |
��ͼ4����4��t��7ʱ��BP=t��
��GP=
| 1 |
| 2 |

��CN=3-��t-4��=7-t��
��NR=
| 28-4t |
| 3 |
��S=
(
| ||
| 2 |
(4+
| ||
| 2 |
| 11 |
| 12 |
| 28 |
| 3 |
| 22 |
| 3 |
��ͼ5����7��t��8ʱ��BP=t��
��GP=
| 1 |
| 2 |
��S=
(
| ||
| 2 |
| 3��4 |
| 2 |
| 1 |
| 4 |
��S=
|
��3���ߡ�PEF+��QEF=180��=��QDF+��QEF
 ��
�����PEF=��QDF=2��ADB=��ABC��
��cos��ABC=cos��PEF=
| 3 |
| 5 |
�ɣ�1����֪EP=
| 1 |
| 2 |
| 1 |
| 2 |
��EF=EQ=PQ-EP=4-
| 1 |
| 2 |
����ͼ6����EF=EPʱ��4-
| 1 |
| 2 |
| 1 |
| 2 |
��t=4��
����ͼ7����FE=FPʱ����FR��EP������ΪR��
��ER=
| 1 |
| 2 |
| 3 |
| 5 |
��
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
��t=
| 48 |
| 11 |
 ����ͼ8����PE=PFʱ����PS��EF������ΪS��
����ͼ8����PE=PFʱ����PS��EF������ΪS����ES=
| 1 |
| 2 |
| 3 |
| 5 |
��
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
��t=
| 40 |
| 11 |
�൱t=4��
| 48 |
| 11 |
| 40 |
| 11 |
������������һ���������ۺ����⣬�����˶�����������ã�����ֱ�����ε����ʵ����ã�ȫ�������ε��ж������ʵ����ã��ֶκ��������ã����������ε����ʵ����ã������ʱ��ֶκ���ʱ����������ε�����ǹؼ����ڵ��������õ��������ε����ʽ���ǹؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��ͼ��������ABCD�У�AD��BC��AB=DC=AD��AC=BC�����ACB�Ķ�����
��ͼ��������ABCD�У�AD��BC��AB=DC=AD��AC=BC�����ACB�Ķ����� ��ͼ��������ABCD�У�AD��BC��BC=30cm������M��A�㿪ʼ��AD����D��1cm/s���ٶ��˶�������N��C�㿪ʼ��CB����B��3cm/s���ٶ��˶���M��N�ֱ��A��Cͬʱ������������һ�㵽�˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt s��tΪ��ֵʱ���ı���ABNM��ƽ���ı��Σ�
��ͼ��������ABCD�У�AD��BC��BC=30cm������M��A�㿪ʼ��AD����D��1cm/s���ٶ��˶�������N��C�㿪ʼ��CB����B��3cm/s���ٶ��˶���M��N�ֱ��A��Cͬʱ������������һ�㵽�˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊt s��tΪ��ֵʱ���ı���ABNM��ƽ���ı��Σ� ��ͼ��������ABCD�У�AD��BC��AB=DC����ACB=40�㣬��ACD=30�㣬���B=
��ͼ��������ABCD�У�AD��BC��AB=DC����ACB=40�㣬��ACD=30�㣬���B=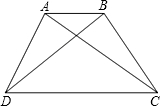 ��ͼ��������ABCD�У�AB��CD��AD=BC��AC��BD��AB+CD=20��������ABCD�������
��ͼ��������ABCD�У�AB��CD��AD=BC��AC��BD��AB+CD=20��������ABCD������� ��ͼ����������ABCD�У�AD=2��BC=6����DF=2��������DC=
��ͼ����������ABCD�У�AD=2��BC=6����DF=2��������DC=