题目内容
【题目】如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:
(1)求抛物线的解析式.
(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.

【答案】(1)y=x2+6x+5;(2)28
【解析】(1)由对称轴公式可求出b值,再将点A的坐标及b值代入到抛物线中求出c,即可得到抛物线的解析;(2)通过C点坐标、对称轴及点B的坐标求出CD及CD上的高即可求出△BCD的面积.
解:(1)把点A(﹣4,﹣3)代入y=x2+bx+c得:
16﹣4b+c=﹣3,
c﹣4b=﹣19,
∵对称轴是x=﹣3,
∴﹣![]() =﹣3,
=﹣3,
∴b=6,
∴c=5,
∴抛物线的解析式是y=x2+6x+5
(2)∵CD∥x轴,
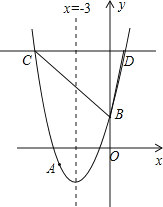
∴点C与点D关于x=﹣3对称,
∵点C在对称轴左侧,且CD=8,
∴点C的横坐标为﹣7,
∴点C的纵坐标为(﹣7)2+6×(﹣7)+5=12,
∵点B的坐标为(0,5),
∴△BCD中CD边上的高为12﹣5=7,
∴△BCD的面积=![]() ×8×7=28.
×8×7=28.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目