题目内容
【题目】如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.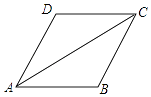
(1)求证:AB=BC;
(2)若AB=4,AC=4 ![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
【答案】
(1)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAC=∠BCA,
∵∠BAC=∠DAC,
∴∠BAC=∠BCA,
∴AB=BC;

(2)
解:连接BD交AC于O,如图所示:
∵四边形ABCD是平行四边形,AB=BC,
∴四边形ABCD是菱形,
∴AC⊥BD,OA=OC= ![]() AC=2
AC=2 ![]() ,OB=OD=
,OB=OD= ![]() BD,
BD,
∴OB= ![]() ═2,
═2,
∴BD=2OB=4,
∴平行四边形ABCD的面积= ![]() ACBD=
ACBD= ![]() ×
× ![]()
【解析】(1)根据平行四边形的性质得出AD∥BC,根据平行线的性质得出∠DAC=∠BCA,求出∠BAC=∠BCA即可;(2)求出四边形ABCD是菱形,根据勾股定理求出BO,求出BD,根据面积公式求出即可.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
【题目】下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
卖钱额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;
(3)当橘子卖出50千克时,预测卖钱额是多少?

