题目内容
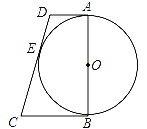
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB、AC于点E、G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.
其中正确结论的序号是( )

A. ①②③④⑤ B. ①②③④ C. ①③④⑤ D. ①④⑤
【答案】D
【解析】∵在正方形纸片ABCD中,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,
∴∠GAD=45°,∠ADG=![]() ∠ADO=22.5°,
∠ADO=22.5°,
∴∠AGD=112.5°,
∴①正确.
∵tan∠AED=![]() ,AE=EF<BE,
,AE=EF<BE,
∴AE<![]() AB,
AB,
∴tan∠AED=![]() >2,
>2,
∴②错误.
∵AG=FG>OG,△AGD与△OGD同高,
∴S△AGD>S△OGD,
∴③错误.
根据题意可得:AE=EF,AG=FG,
又∵EF∥AC,
∴∠FEG=∠AGE,
又∵∠AEG=∠FEG,
∴∠AEG=∠AGE,
∴AE=AG=EF=FG,
∴四边形AEFG是菱形,
∴④正确.
∵在等腰直角三角形BEF和等腰直角三角形OFG中,BE2=2EF2=2GF2=2×2OG2,
∴BE=2OG.
∴⑤正确.
故其中正确结论的序号是:①④⑤.
故选:D.

练习册系列答案
相关题目