题目内容
【题目】判定一个三角形是不是等腰三角形，我们经常利用以下的判定方法：“如果一个三角形有两个角相等，那么这两个角所对的边也相等”，请你利用以上判定方法解决下列问题
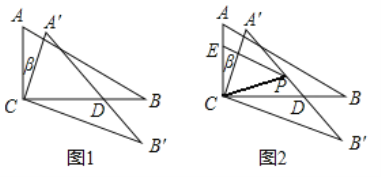
如图1，在△ABC中，∠ACB=90°，∠B=30°，将△ABC绕顶点C顺时针旋转，旋转角为β
（0°＜β＜180°），得到△A′B′C
（1）设A′B′与CB相交于点D，
①当旋转角为β=25°，∠B′DB= °；
②当AB∥CB′ 时，求证：D是A′B′ 的中点；
（2）如图2，E是AC边上的点，且
，P是A′B′边上的点，且∠A′PC=60°，连接EP、CP，已知AC=10，①当β= °时，EP长度最大，最大值为 ；
②当β= °时，△ECP的面积最大，最大值为 。
【答案】（1）①55°；②详见解析；（2）①当β= 120°时，EP长度最大，最大值为16；②当β=30°时，△ECP的面积最大，最大值为30 .
【解析】试题分析：（1）①根据旋转的性质，旋转前后两个图形全等，则∠A'B'C=∠B，∠ACA′=∠B′CB，根据三角形的外角等于不相邻的两个内角和即可得到结论；
②根据平行的性质证明∠BCB'=∠B'，然后证明∠A'DC=∠A'，根据等角对等边即可证得；
（2）①∠A′PC=60°时易证△A'CP是等边三角形，当A、C、P在一条直线上时，EP的长度最大，据此即可求解；
②由PC=10是固定不变的，故只要PC边上的高最大即可，当EC⊥PC时，PC边上的高的最大值为EC， 此时∠ECP=90°，即可得到结论．
试题解析：解：（1）①∵∠ACB=∠A′CB′=90°，∴∠ACA′=∠B′CB=25°，∵∠B′=∠B=30°，∴∠B′DB=∠B′+∠B′CB=30°+25°=55°；
②∵AB∥CB′，∴∠DCB′=∠B=∠B′=30°，∴DC=DB′，
又∠DCA′=∠A′C B′-∠DCB′=90°-30°=60°=∠A′，∴DC=DA′，∴DB′=DA′（等量代换）．即D是A′B′ 的中点；
（2）①∵AE=
AC，AC=10，∴AE=4，EC=6．∵∠A′PC=60°，∠A'=∠A=60°，∴△A'CP是等边三角形，∴CP=CA'=10，∠A'CP=60°，∵当A、C、P在一条直线上时，EP的长度最大，即当β=180°﹣60°=120°时，EP长度最大，最大值为EC+AC=6+10=16．
②∵△A'CP是等边三角形，∴CP=CA'=10，∠A'CP=60°．∵PC=10是固定不变的，∴只要PC边上的高最大即可，当EC⊥PC时，PC边上的高的最大值为EC， 此时∠ECP=90°，∴β=90°-60°=30°，△ECP的面积=
CE×PC=
×6×10=30．
