ƒøƒ⁄»ð
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() £¨æ≠π˝µ„
£¨æ≠π˝µ„![]() £¨
£¨![]() £¨
£¨![]() »˝µ„£Æ
»˝µ„£Æ
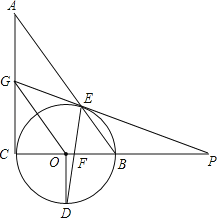
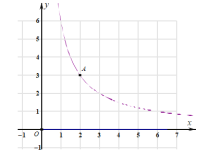
![]() «Û≈◊ŒÔœþµƒΩ‚Œˆ Ωº∞∂•µ„Mµƒ◊¯±Í£ª
«Û≈◊ŒÔœþµƒΩ‚Œˆ Ωº∞∂•µ„Mµƒ◊¯±Í£ª
![]() ¡¨Ω”AC°¢MB£¨PŒ™œþ∂ŒMB…œµƒ“ª∏ˆ∂ص„£®≤ª”ε„M°¢B÷ÿ∫œ£©£¨π˝µ„P◊˜x÷·µƒ¥πœþPQ£¨»ÙOQ=a£¨Àƒ±þ–ŒACPQµƒ√ʪ˝Œ™s£¨«ÛaŒ™∫Œ÷µ ±£¨√ʪ˝s◊Ó¥Û£ª
¡¨Ω”AC°¢MB£¨PŒ™œþ∂ŒMB…œµƒ“ª∏ˆ∂ص„£®≤ª”ε„M°¢B÷ÿ∫œ£©£¨π˝µ„P◊˜x÷·µƒ¥πœþPQ£¨»ÙOQ=a£¨Àƒ±þ–ŒACPQµƒ√ʪ˝Œ™s£¨«ÛaŒ™∫Œ÷µ ±£¨√ʪ˝s◊Ó¥Û£ª
![]() µ„N «≈◊ŒÔœþ…œµ⁄ÀƒœÛœÞµƒ“ª∏ˆ∂®µ„£¨◊¯±ÍŒ™
µ„N «≈◊ŒÔœþ…œµ⁄ÀƒœÛœÞµƒ“ª∏ˆ∂®µ„£¨◊¯±ÍŒ™![]() £¨π˝µ„C◊˜÷±œþ
£¨π˝µ„C◊˜÷±œþ![]() ÷·£¨∂ص„
÷·£¨∂ص„![]() ‘⁄÷±œþl…œ£¨∂ص„
‘⁄÷±œþl…œ£¨∂ص„![]() ‘⁄x÷·…œ£¨¡¨Ω”PM°¢PQ°¢NQ£¨µ±mŒ™∫Œ÷µ ±£¨
‘⁄x÷·…œ£¨¡¨Ω”PM°¢PQ°¢NQ£¨µ±mŒ™∫Œ÷µ ±£¨![]() µƒ∫Õ◊Ó–°£¨≤¢«Û≥ˆ
µƒ∫Õ◊Ó–°£¨≤¢«Û≥ˆ![]() ∫Õµƒ◊Ó–°÷µ£Æ
∫Õµƒ◊Ó–°÷µ£Æ

°æ¥∞∏°ø£®1£©![]() £ªM£®1,4£©
£ªM£®1,4£©
£®2£©µ±![]() £¨
£¨![]() √ʪ˝◊Ó¥Û£¨◊Ó¥ÛŒ™
√ʪ˝◊Ó¥Û£¨◊Ó¥ÛŒ™![]() .
.
£®£≥£©![]()
°æΩ‚Œˆ°ø
£®1£©≈◊ŒÔœþ![]() π˝
π˝![]() £¨
£¨![]() £¨
£¨![]() ø…«Ûµ√Ω‚Œˆ Ω£ª
ø…«Ûµ√Ω‚Œˆ Ω£ª
£®2£©Ω´![]() ”√∫¨
”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ£¨≤¢≈‰∑Ω≥…∂•µ„ Ω«Û≥ˆ◊Ó¥Û÷µ£ª
µƒ¥˙ ˝ Ω±Ì æ£¨≤¢≈‰∑Ω≥…∂•µ„ Ω«Û≥ˆ◊Ó¥Û÷µ£ª
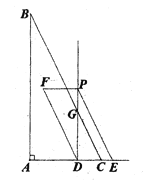
£®3£©∏˘æð—°÷∑‘Ï«≈ƒ£–Õ£¨Ω´∂•µ„![]() œÚœ¬∆Ω“∆»˝∏ˆµ•Œªµ√
œÚœ¬∆Ω“∆»˝∏ˆµ•Œªµ√![]() £¨µ±
£¨µ±![]() ‘⁄Õ¨“ªÃı÷±œþ…œ ±£¨
‘⁄Õ¨“ªÃı÷±œþ…œ ±£¨![]() »°µ√◊Ó–°÷µ.
»°µ√◊Ó–°÷µ.
(1)°þ≈◊ŒÔœþ![]() æ≠π˝µ„
æ≠π˝µ„![]() £¨
£¨![]() £¨
£¨![]() ,
,
°ý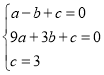 Ω‚µ√
Ω‚µ√
°ý![]() =
=![]() ,∂•µ„Mµƒ◊¯±ÍŒ™£®1,4£©
,∂•µ„Mµƒ◊¯±ÍŒ™£®1,4£©
£®2£©¡¨Ω”AC°¢MB£¨PŒ™œþ∂ŒMB…œµƒ“ª∏ˆ∂ص„£®≤ª”ε„M°¢B÷ÿ∫œ£©£¨π˝µ„P◊˜x÷·µƒ¥πœþPQ.…ËPµ„µƒ◊¯±ÍŒ™![]() £¨»ÁÕºÀ˘ æ.
£¨»ÁÕºÀ˘ æ.

°þP‘⁄÷±œþMB…œ£¨![]() £¨
£¨![]() £¨…Ë÷±œþMBŒ™
£¨…Ë÷±œþMBŒ™![]()
![]() Ω‚µ√
Ω‚µ√![]()
÷±œþMBµƒΩ‚Œˆ ΩŒ™![]() £¨Pµ„◊¯±ÍŒ™
£¨Pµ„◊¯±ÍŒ™![]()
°þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]()
![]()
°ý![]() £¨
£¨![]() £¨
£¨![]()
°þ![]()
’˚¿Ì![]()
°ýº¥µ±![]() £¨
£¨![]() √ʪ˝◊Ó¥Û£¨◊Ó¥ÛŒ™
√ʪ˝◊Ó¥Û£¨◊Ó¥ÛŒ™![]() .
.
£®3£©Ω´∂•µ„![]() œÚœ¬∆Ω“∆»˝∏ˆµ•Œªµ√
œÚœ¬∆Ω“∆»˝∏ˆµ•Œªµ√![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ÷·”⁄µ„
÷·”⁄µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ»ÁÕºÀ˘ 棨‘Ú
£Æ»ÁÕºÀ˘ 棨‘Ú![]() .
.
°þ![]() £¨
£¨![]()
°ý![]() ÷·£¨«“
÷·£¨«“![]()
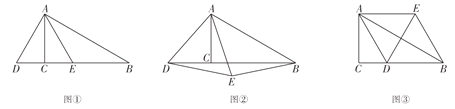
°ý![]() £¨Àƒ±þ–Œ
£¨Àƒ±þ–Œ![]() Œ™∆Ω––Àƒ±þ–Œ
Œ™∆Ω––Àƒ±þ–Œ
°ý![]() ,”–Õº÷™
,”–Õº÷™![]() »˝µ„π≤œþ ±£¨
»˝µ„π≤œþ ±£¨![]() »°◊Ó–°÷µ.
»°◊Ó–°÷µ.
…Ë÷±œþ![]() µƒΩ‚Œˆ ΩŒ™
µƒΩ‚Œˆ ΩŒ™![]() £¨Ω´µ„
£¨Ω´µ„![]() £¨N
£¨N![]()
«Ûµ√÷±œþ![]() µƒΩ‚Œˆ ΩŒ™
µƒΩ‚Œˆ ΩŒ™![]() £¨
£¨
µ±![]() ±£¨
±£¨![]() £¨º¥
£¨º¥![]() £¨º¥
£¨º¥![]() £¨
£¨
¥À ±π˝µ„![]() ◊˜
◊˜![]() ÷·Ωª
÷·Ωª![]() —”≥§œþ”ε„
—”≥§œþ”ε„![]() £¨
£¨
‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨
°ý![]() ,
,
°ý![]() ,º¥
,º¥![]() ,
,
°ýµ±![]() ±£¨
±£¨![]() µƒ◊Ó–°÷µŒ™
µƒ◊Ó–°÷µŒ™![]() .
.

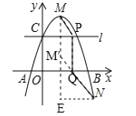
°æƒø°ø“—÷™“ª∏ˆ∂˛¥Œ∫Ø ˝ÕºœÛ…œ≤ø∑÷µ„µƒ∫·◊¯±Í![]() ”Î◊ð◊¯±Í
”Î◊ð◊¯±Í![]() µƒ∂‘”¶÷µ»Á±ÌÀ˘ æ£∫
µƒ∂‘”¶÷µ»Á±ÌÀ˘ æ£∫
| °≠ | ©Å3 | ©Å2 | ©Å1 | 0 | 1 | °≠ |
| °≠ | 0 | ©Å3 | ©Å4 | ©Å3 | 0 | °≠ |
(1)«Û’‚∏ˆ∂˛¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
(2)‘⁄∏¯∂®µƒ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–ª≠≥ˆ’‚∏ˆ∂˛¥Œ∫Ø ˝µƒÕºœÛ£ª
(3)µ±![]() ±£¨÷±Ω”–¥≥ˆ
±£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ