Question

【题目】如图，以△ABC的边AB、AC为边向外作等边三角形△ABD与△ACE，线段BE交DC于点F，下列结论：①CD＝BE；②FA平分∠BAC；③∠BFC＝120°，④FA+FB＝FD，其中正确有（　　）个．

A.4个B.3个C.2个D.1个

Answer 1

【答案】B

【解析】

证明△ADC≌△ABE，根据全等三角形的性质可推出①③正确，在DF上取一点K，使得FK=FA，可得△AKF是等边三角形，再证明△DAK≌△BAF，可推出④正确，证明AF平分∠DFE，根据三角形外角的性质可推出②不一定成立，故②错误.

解：如图设AC交BE于点O．

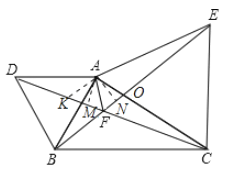
∵△ABD，△ACE都是等边三角形，
∴AD=AB，AE=AC，∠DAB=∠EAC=60°，

∴∠DAC=∠EAB，
∴△ADC≌△ABE（SAS），
∴CD=BE，∠AEB=∠ACD，∠ABE=∠ADC，故①正确
作AM⊥CD于M，AN⊥BE于N，
∵△ADC≌△ABE，
∴AM=AN，
∴AF平分∠DFE，∠DFA=∠EFA，

在△ABF和△AFC中，

∠BAF=∠EFA-∠ABF，∠CAF=∠DFA-∠ACD，

∵∠ACD和∠ABF不一定相等，

∴无法判断∠BAF和∠CAF相等，即无法判断AF平分∠BAC，故②错误，
∵∠AOE=∠COF，
∴∠OAE=∠OFC=60°，
∴∠BFC=120°，故③正确，
在DF上取一点K，使得FK=FA，
∵∠AFK=∠AFN=60°，
∴△AKF是等边三角形，

∴AF=AK, ∠DAB=∠KAF =60°

∴∠DAK=∠BAF

又∵AB=AD
∴△DAK≌△BAF(SAS)，
∴DK=BF，
∴DF=DK+KF=FA+FB，故④正确，
故①③④正确选：B．