题目内容
【题目】如图,已知AB∥CD,O为∠CAB、∠ACD的角平分线的交点,OE⊥AC于E,且OE=2,CO=3,则两平行线间AB、CD的距离等于 . 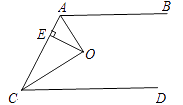
【答案】4
【解析】如图,过点O作MN,MN⊥AB于M,交CD于N,
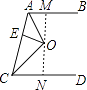
∵AB∥CD,
∴MN⊥CD,
∵AO是∠BAC的平分线,OM⊥AB,OE⊥AC,OE=2,
∴OM=OE=2,
∵CO是∠ACD的平分线,OE⊥AC,ON⊥CD,
∴ON=OE=2,
∴MN=OM+ON=4,
即AB与CD之间的距离是4.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握平行线之间的距离(两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离)的相关知识才是答题的关键.

练习册系列答案
相关题目