题目内容
【题目】如图所示,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )

A.20°B.30°C.25°D.15°
【答案】A
【解析】
在DC上取DE=DB.连接AE,先证明△ABD≌△AED,得出AB=AE,再结合AB+BD=DC根据等量代换可得出AE=EC,再根据等腰三角形的性质以及三角形外角的性质可得出∠B=∠AED=2∠C,从而可得出结果.
解:如图,在DC上取DE=DB,连接AE.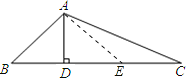
在△ABD和△AED中,
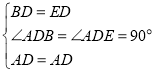 ,
,
∴△ABD≌△AED(SAS).
∴AB=AE,∠B=∠AED.
又∵AB+BD=CD,
∴EC=CD-DE=CD-BD=(AB+BD)-BD=AB=AE,
即EC=AE,
∴∠C=∠CAE,
∴∠B=∠AED=2∠C,
又∵∠B+∠C=180°-∠BAC=60°,
∴∠C=20°,
故选:A.

练习册系列答案
相关题目