题目内容
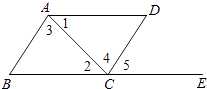
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.

(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF,OD,OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F=![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
【答案】(1)证明见解析;(2)EF2=4ODOP,证明见解析;(3)![]() ,
,![]() .
.
【解析】
试题分析:(1)连接OB,根据垂径定理的知识,得出OA=OB,∠POA=∠POB,从而证明△PAO≌△PBO,然后利用全等三角形的性质结合切线的判定定理即可得出结论;
(2)先证明△OAD∽△OPA,由相似三角形的性质得出OA与OD、OP的关系,然后将EF=2OA代入关系式即可;
(3)根据题意可确定OD是△ABC的中位线,设AD=x,然后利用三角函数的知识表示出FD、OA,在Rt△AOD中,由勾股定理解出x的值,从而能求出cos∠ACB,再由(2)可得OA2=ODOP,代入数据即可得出PE的长.
试题解析:(1)如图,连接OB,
∵PB是⊙O的切线,∴∠PBO=90°.
∵OA=OB,BA⊥PO于D,∴AD=BD,∠POA=∠POB.
又∵PO=PO,∴△PAO≌△PBO(SAS).
∴∠PAO=∠PBO=90°. ∴直线PA为⊙O的切线.

(2)EF2=4ODOP,证明如下:
∵∠PAO=∠PDA=90°,∴∠OAD+∠AOD=90°,∠OPA+∠AOP=90°.
∴∠OAD=∠OPA. ∴△OAD∽△OPA. ∴![]() ,即OA2=ODOP.
,即OA2=ODOP.
又∵EF=2OA,∴EF2=4ODOP.
(3)∵OA=OC,AD=BD,BC=6,∴OD=![]() BC=3(三角形中位线定理).
BC=3(三角形中位线定理).
设AD=x,
∵tan∠F=![]() ,∴FD=2x,OA=OF=2x﹣3.
,∴FD=2x,OA=OF=2x﹣3.
在Rt△AOD中,由勾股定理,得(2x﹣3)2=x2+32,
解得,x1=4,x2=0(不合题意,舍去).∴AD=4,OA=2x﹣3=5.
∵AC是⊙O直径,∴∠ABC=90°.
又∵AC=2OA=10,BC=6,∴cos∠ACB=![]() .
.
∵OA2=ODOP,∴3(PE+5)=25.∴PE=![]() .
.

【题目】某政府部门进行公务员招聘考试,其中三人中录取一人,他们的成绩如下:
人 | 测试成绩 | ||
题目 | 甲 | 乙 | 丙 |
文化课知识 | 74 | 87 | 69 |
面试 | 58 | 74 | 70 |
平时表现 | 87 | 43 | 65 |
(1)按照平均成绩甲、乙、丙谁应被录取?
(2)若按照文化课知识、面试、平时表现的成绩已4:3:1的比例录取,甲、乙、丙谁应被录取?