题目内容
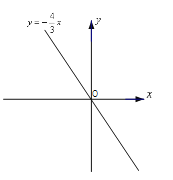
【题目】一次函数y=![]() x的图像如图所示,它与二次函数y=ax2+2ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
x的图像如图所示,它与二次函数y=ax2+2ax+c的图像交于A、B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图像的顶点为D.若点D与点C关于x轴对称,且△ACD的面积等于![]() ,求此二次函数的关系式.
,求此二次函数的关系式.
【答案】(1)点C的坐标为(-1,![]() );(2)
);(2)![]()
【解析】
(1)先求出对称轴为x=2,然后求出与一次函数y=-![]() x的交点,即点C的坐标
x的交点,即点C的坐标
(2)①先求出点D的坐标,然后根据面积为![]() ,得出点A的坐标,最后根据待定系数法求出a的值,即可求出解析式.
,得出点A的坐标,最后根据待定系数法求出a的值,即可求出解析式.
(1)∵抛物线的对称轴为x=![]() =-1.
=-1.
∵将x=-1代入y=![]() x得:y=
x得:y=![]() ,∴点C的坐标为(-1,
,∴点C的坐标为(-1,![]() ).
).
(2)①∵点D与点C关于x轴对称,∴点D的坐标为(-1,-![]() ),∴CD=
),∴CD=![]() .
.
设△ACD的CD边上的高为h,则![]()
![]() h=
h=![]() ,解得h=4
,解得h=4
∴点A的横坐标为-4-1=-5或-1+4=3,则点A的纵坐标为![]() 或-
或-![]() ×3=-4.
×3=-4.
即A(-5,![]() )或(3,-4)
)或(3,-4)
设抛物线的解析式为![]() ,将A(-5,
,将A(-5,![]() )代入得:
)代入得:![]() =
=![]() .
.
解得:![]() ,或将A(3,-4)带入得:-4=a(3+1)2-
,或将A(3,-4)带入得:-4=a(3+1)2-![]() ,解得a=-
,解得a=-![]()
∴抛物线的解析式为![]() 或
或![]() .
.
直线![]() 与抛物线
与抛物线![]() 相切于点A,仍不合题意,应舍去.
相切于点A,仍不合题意,应舍去.
故二次函数的关系式为![]() .
.

 教学练新同步练习系列答案
教学练新同步练习系列答案【题目】小明同学三次到某超市购买A、B两种商品,其中仅有一次是有折扣的,购买数量及消费金额如下表:
类别 次数 | 购买A商品数量(件) | 购买B商品数量(件) | 消费金额(元) |
第一次 | 4 | 5 | 320 |
第二次 | 2 | 6 | 300 |
第三次 | 5 | 7 | 258 |
解答下列问题:
(1)第 次购买有折扣;
(2)求A、B两种商品的原价;
(3)若购买A、B两种商品的折扣数相同,求折扣数;
(4)小明同学再次购买A、B两种商品共10件,在(3)中折扣数的前提下,消费金额不超过200元,求至少购买A商品多少件.