题目内容
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
【答案】(1)①(-2,0),(1,0);②8;(2)所求抛物线解析式为y=2x2+2x-4.
【解析】试题分析: (1)①根据表格中函数值y=0即可得到与x轴的交点坐标;
②观察表格可知抛物线的对称轴为x=![]() ,由此可知(2,8)与(-3,8)关于对称轴对称,从而可得;
,由此可知(2,8)与(-3,8)关于对称轴对称,从而可得;
(2)依题意设抛物线解析式为y=a(x+2)(x-1),代入点(0,-4)即可求得.
试题解析:(1)①观察表格可知当y=0时,x=-2或x=1,所以抛物线与x轴的交点坐标是(-2,0),(1,0),
故答案为:(-2,0),(1,0);
②观察表格可知抛物线的对称轴为x=![]() ,由此可知(2,8)与(-3,8)关于对称轴对称,所以抛物线经过(-3,8),
,由此可知(2,8)与(-3,8)关于对称轴对称,所以抛物线经过(-3,8),
故答案为:8;
(2)依题意设抛物线解析式为y=a(x+2)(x-1),
由点(0,-4)在函数图象上,得-4=a(0+2)×(0-1),
解得a=2,
∴y=2(x+2)(x-1),
即所求抛物线解析式为y=2x2+2x-4.

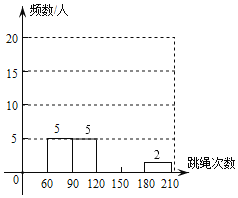
【题目】学校为了了解七年学生跳绳情况,从七年级学生中随机抽查了50名学生进行1分钟跳绳测试,并对测试结果统计后绘制了如下不完整统计图表,请根据图表中的信息解答下列问题.
组别 | 次数 | 频数(人) | 百分比 |
1 | 60≤x<90 | 5 | 10% |
2 | 90≤x<120 | 5 | b |
3 | 120≤x<150 | 18 | 36% |
4 | 150≤x<180 | a | c |
5 | 180≤x<210 | 2 | 4% |
合计 | 50 | 1 | |
(1)直接写出a= ,b= ,c= ;
(2)请补全频数分布直方图;
(3)若该校七年级共有学生400人,请你估计该校七年级学生跳绳次数在90≤x<150范围的学生约有多少人?(