题目内容
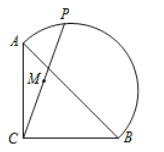
【题目】如图,在等腰Rt△ABC中,AC=BC=2,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是( )
A. π B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】B
【解析】
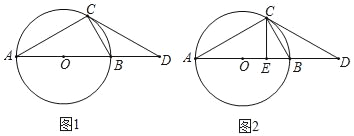
取AB的中点O、AE的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图,利用等腰直角三角形的性质得到![]() ,则
,则![]() ,
,![]() ,再根据等腰三角形的性质得OM⊥PC,则∠CMO=90°,于是根据圆周角定理得到点M在以OC为直径的圆上,由于点P点在A点时,M点在E点;点P点在B点时,M点在F点,则利用四边形CEOF为正方得到EF=OC=
,再根据等腰三角形的性质得OM⊥PC,则∠CMO=90°,于是根据圆周角定理得到点M在以OC为直径的圆上,由于点P点在A点时,M点在E点;点P点在B点时,M点在F点,则利用四边形CEOF为正方得到EF=OC=![]() ,所以M点的路径为以EF为直径的半圆,然后根据圆的周长公式计算点M运动的路径长.
,所以M点的路径为以EF为直径的半圆,然后根据圆的周长公式计算点M运动的路径长.

取AB的中点O、AE的中点E、BC的中点F,连结OC、OP、OM、OE、OF、EF,如图,
∵在等腰Rt△ABC中,AC=BC=2,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵M为PC的中点,
∴OM⊥PC,
∴∠CMO=90°,
∴点M在以PC为直径的圆上,
点P点在A点时,M点在E点;点P点在B点时,M点在F点,易得四边形CEOF为正方形,EF=OC=![]() ,
,
∴M点的路径为以EF为直径的半圆,
∴点M运动的路径长=![]() .
.
故选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目