Question

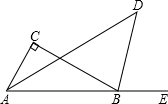
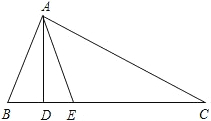
如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．
（1）求∠BAE的度数；
（2）求∠DAE的度数；
（3）探究：有同学认为，不论∠B，∠C的度数是多少，都有∠DAE=

1

2

（∠B-∠C）成立，你同意吗？你能说出成立或不成立的理由吗？

Answer 1

（1）∵在△ABC中，∠B=70°，∠C=30°，
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°，
∵AE平分∠BAC，
∴∠BAE=

1

2

∠BAC=

1

2

×80°=40°；

（2）∵AD⊥BC，∠B=70°，
∴∠BAD=90°-∠B=90°-70°=20°，
∵∠BAE=40°，
∴∠DAE=∠BAE-∠BAD=40°-20°=20°；

（3）成立．
∵AE平分∠BAC，
∴∠BAE=

1

2

（180°-∠B-∠C），
∵AD⊥BC，
∴∠BAD=90°-∠B，
∴∠DAE=∠BAE-∠BAD=

1

2

（180°-∠B-∠C）-90°+∠B=

1

2

（∠B-∠C）．