题目内容
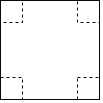
【题目】如图,把一边长为x厘米的正方形纸板的四个角各剪去一个边长为y厘米的小正方形,然后把它折成一个无盖纸盒.
(1)该纸盒的高是_____厘米,底面积是_____________平方厘米;
(2)求该纸盒的全面积(外表面积);
(3)为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时x与y之间的倍数关系.(直接写出答案即可)
【答案】(1)y,(x-2y)2;(2) x2-4y2;(3) x=4y
【解析】试题分析:(1)由图可得;
(2)根据纸盒的全面积=大正方形面积-4个小正方形面积,计算即可;
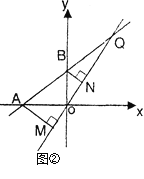
(3)如图由题意AD=2AE=2DF,推出EF=2AD=4AE,由此即可解决问题;
试题解析:
(1)由图可得:高是y,底面积(x-2y)(x-2y)=(x-2y)2;
故答案是:y,(x-2y)2;
(2)x2-4y2
所以该纸盒的全面积为(x2-4y2)cm2
(3)结论:x=4y.
理由:如图由题意AD=2AE=2DF,
∴EF=2AD=4AE,
∵EF=x,AE=y,
∴x=4y.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目