Question

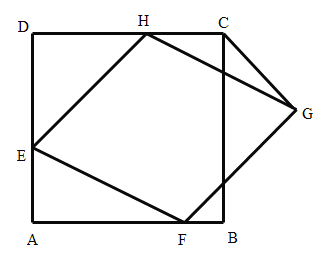
【题目】如图，在正方形中，边长为，菱形的三个顶点分别在正方形的边上连接，则的面积等于_____．

Answer 1

【答案】2

【解析】

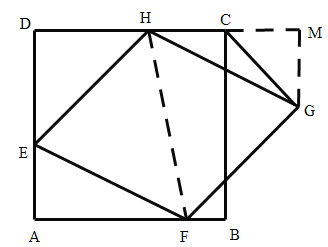
如图，连接HF，过点G作GM⊥DC交DC延长线于点M，根据正方形的性质及平行线的性质得到∠AFH=∠MHF，根据菱形的性质得到∠EFH=∠GHF，进而证明∠AFE=∠MHG，从而证明△AFE≌△MHG（AAS），得到MG=2，计算出HC，再根据三角形的面积公式即可解答．

解：如图，连接HF，过点G作GM⊥DC交DC延长线于点M，则∠M=90°，

∵四边形ABCD是正方形，边长为5，

∴AD=DC=5，∠A=90°，，

∴∠AFH=∠MHF，

∵四边形是菱形，

∴EF=HG，，

∴∠EFH=∠GHF，

∴∠AFH-∠EFH =∠MHF-∠GHF，

即∠AFE=∠MHG，

在△AFE与△MHG中，

∠A=∠M=90°，∠AFE=∠MHG，EF=HG，

∴△AFE≌△MHG（AAS），

∴AE=MG=2，

∵DH=3，

∴HC=5-3=2，

∴S△HCG=，

故答案为：2．