题目内容
【题目】“绿水青山就是金山银山”，为保护生态环境，A，B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
（1）若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元；
（2）在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，则至少安排多少人清理养鱼网箱？
（3）在第（2）问的条件下，若要求清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？
【答案】（1）2000元；3000元 （2）18人 （3）见解析
【解析】
（1）设清理养鱼网箱的人均费用为
元，清理捕鱼网箱的人均费用为
元，根据题意列出二元一次方程组再进行求解即可；
（2）设
人清理养鱼网箱，则
人清理捕鱼网箱，根据题意列一元一次不等式即可求解；
（3）根据题意列出不等式，再根据（2）的结论求不等式整数解即可．
解:（1）设清理养鱼网箱的人均费用为元，清理捕鱼网箱的人均费用为元，
根据题意，得：
，
解得：
，
答：清理养鱼网箱的人均费用为2000元，清理捕鱼网箱的人均费用为3000元；
（2）设人清理养鱼网箱，则人清理捕鱼网箱，
根据题意，得：
解得：
答：至少安排18人清理养鱼网箱．
（3）根据题意，得：
解得：
由（2）知
所以
∵为整数，
∴
或
则分配清理人员方案有两种：
方案一：18人清理养鱼网箱，22人清理捕鱼网箱；
方案二：19人清理养鱼网箱，21人清理捕鱼网箱．
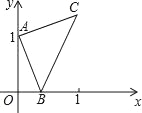
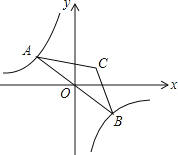
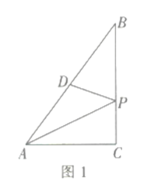
阅读快车系列答案
【题目】如图1，在
中，
为
的中点，
是
边上一动点，连接
．若
设 
(当点与点
重合时，
的值为
)，
．
小明根据学习函数的经验，对函数
随自变量的变化而变化的规律进行了探究．
下面是小明的探究过程，请补充完整．
通过取点、画图、计算，得到了与的几组值，如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
说明：补全表格时，相关数值保留一位小数．
(参考数据：
) ．
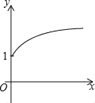
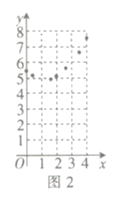
如图2，描出剩余的点，并用光滑的曲线画出该函数的图象．
观察图象，下列结论正确的有 _ ．
①函数有最小值，没有最大值
②函数有最小值，也有最大值
③当
时，随着的增大而增大
④当
时，随着的增大而减小
