题目内容
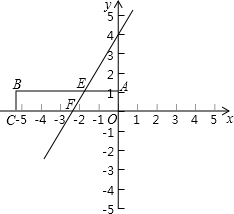
如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3
,1)、C(-3
,0)、O(0,0).将此矩形沿着过E(-
,1)、F(-
,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
| 3 |
| 3 |
| 3 |
4
| ||
| 3 |
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.

(1)由于折痕所在直线EF过E(-
,1)、F(-
,0),则有:
∴设直线EF的解析式为y=kx+b,
∴
;
解得k=
,b=4,
所以直线EF的解析式为:y=
x+4.
(2)设矩形沿直线EF向右下方翻折后,B、C的对应点为B′(x1,y1),C′(x2,y2);
过B′作B′A′⊥AE交AE所在直线于A′点;
∵B′E=BE=2
,∠B′EF=∠BEF=60°,
∴∠B′EA′=60°,
∴A′E=
,B′A′=3;
∴A与A′重合,B′在y轴上;
∴x1=0,y1=-2,
即B′(0,-2);【此时需说明B′(x1,y1)在y轴上】.
设二次函数解析式为:y=ax2+bx+c,抛物线过B(-3
,1)、E(-
,1)、B′(0,-2);
得到
,
解得
∴该二次函数解析式y=-
x2-
x-2;
(3)能,可以在直线EF上找到P点;
连接B′C交EF于P点,再连接BP;
由于B′P=BP,此时点P与C、B′在一条直线上,故BP+PC=B′P+PC的和最小;
由于BC为定长,所以满足△PBC周长最小;
设直线B′C的解析式为:y=kx+b,则有:
,
解得
;
∴直线B′C的解析式为:y=-
x-2;
又∵P为直线B′C和直线EF的交点,
∴
,
解得
;
∴点P的坐标为(-
,-
).
| 3 |
4
| ||
| 3 |
∴设直线EF的解析式为y=kx+b,
∴
|
解得k=
| 3 |
所以直线EF的解析式为:y=
| 3 |
(2)设矩形沿直线EF向右下方翻折后,B、C的对应点为B′(x1,y1),C′(x2,y2);
过B′作B′A′⊥AE交AE所在直线于A′点;
∵B′E=BE=2
| 3 |

∴∠B′EA′=60°,
∴A′E=
| 3 |
∴A与A′重合,B′在y轴上;
∴x1=0,y1=-2,
即B′(0,-2);【此时需说明B′(x1,y1)在y轴上】.
设二次函数解析式为:y=ax2+bx+c,抛物线过B(-3
| 3 |
| 3 |
得到
|
解得
|
∴该二次函数解析式y=-
| 1 |
| 3 |
4
| ||
| 3 |
(3)能,可以在直线EF上找到P点;
连接B′C交EF于P点,再连接BP;
由于B′P=BP,此时点P与C、B′在一条直线上,故BP+PC=B′P+PC的和最小;
由于BC为定长,所以满足△PBC周长最小;
设直线B′C的解析式为:y=kx+b,则有:
|
解得
|
∴直线B′C的解析式为:y=-
2
| ||
| 9 |
又∵P为直线B′C和直线EF的交点,
∴
|
解得
|
∴点P的坐标为(-
18
| ||
| 11 |
| 10 |
| 11 |

练习册系列答案
相关题目



 多少?
多少? 生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.
生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.