题目内容
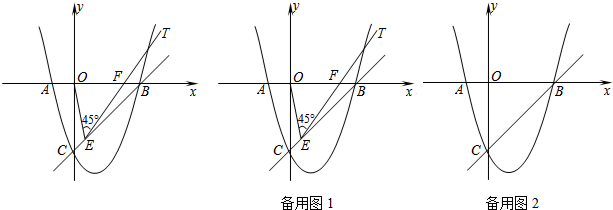
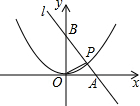
如图已知点A(-2,4)和点B(1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形AA′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.

(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形AA′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
(1)由于抛物线经过A(-2,4)和点B(1,0),则有:
,解得
;
故m=-
,n=4.
(2)由(1)得:y=-
x2-
x+4=-
(x+1)2+
;
由A(-2,4)、B(1,0),可得AB=
=5;
若四边形AA′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=-
(x+1-5)2+
=-
(x-4)2+
.
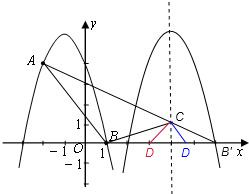 (3)由(2)得:平移后抛物线的对称轴为:x=4;
(3)由(2)得:平移后抛物线的对称轴为:x=4;
∵A(-2,4),B′(6,0),
∴直线AB′:y=-
x+3;
当x=4时,y=1,故C(4,1);
所以:AC=3
,B′C=
,BC=
;
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
=
,即
=
,B′D=3,
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
=
,即
=
,B′D=
,
此时D(
,0);
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(
,0).
|
|
故m=-
| 4 |
| 3 |
(2)由(1)得:y=-
| 4 |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
由A(-2,4)、B(1,0),可得AB=
| (1+2)2+(0-4)2 |
若四边形AA′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=-
| 4 |
| 3 |
| 16 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
 (3)由(2)得:平移后抛物线的对称轴为:x=4;
(3)由(2)得:平移后抛物线的对称轴为:x=4;∵A(-2,4),B′(6,0),
∴直线AB′:y=-
| 1 |
| 2 |
当x=4时,y=1,故C(4,1);
所以:AC=3
| 5 |
| 5 |
| 10 |
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
| B′C |
| AB |
| B′D |
| AC |
| ||
| 5 |
| B′D | ||
3
|
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
| B′C |
| AC |
| B′D |
| AB |
| ||
3
|
| B′D |
| 5 |
| 5 |
| 3 |
此时D(
| 13 |
| 3 |
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(
| 13 |
| 3 |

练习册系列答案
相关题目