题目内容
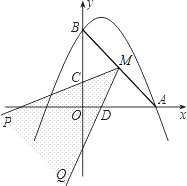
如图,抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)抛物线上是否存在一点Q,使△QMB与△PMB的面积相等?若存在,求点Q的坐标;若不存在,说明理由;
(3)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相等?若存在,直接写出点R的坐标;若不存在,说明理由.
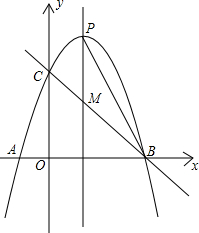
(1)求该抛物线的解析式;
(2)抛物线上是否存在一点Q,使△QMB与△PMB的面积相等?若存在,求点Q的坐标;若不存在,说明理由;
(3)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相等?若存在,直接写出点R的坐标;若不存在,说明理由.

(1)把三点代入抛物线解析式
,
即得:
,
所以二次函数式为y=-x2+2x+3;
(2)由y=-x2+2x+3=-(x-1)2+4,
则顶点P(1,4),
由B,C两点坐标可求直线BC解析式为y=-x+3,
设过点P与直线BC平行的直线为:y=-x+b′,
将点P(1,4)代入,得y=-x+5,
则过点P与直线BC平行的直线与抛物线联立,有则存在点Q,
-x2+2x+3=-x+5,
即x2-3x+2=0,
解得x=1或x=2,
代入直线则得点(1,4)或(2,3),
已知点P(1,4),
所以点Q(2,3),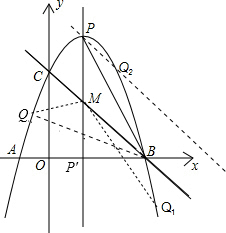
由对称轴及直线BC解析式可知M(1,2),PM=2,
设过P′(1,0)且与BC平行的直线为y=-x+f,
将P′代入,得y=-x+1,
联立
,解得
或
,
∴Q(2,3)或(
,
)或Q(
,
);
(3)由题意求得直线BC代入x=1,则y=2,
∴M(1,2),
由点M,P的坐标可知:
点R存在,即过点M平行于x轴的直线,
则代入y=2,x2-2x-1=0,
解得x=1-
(在对称轴的左侧,舍去),x=1+
,
即点R(1+
,2).
|
即得:
|
所以二次函数式为y=-x2+2x+3;
(2)由y=-x2+2x+3=-(x-1)2+4,
则顶点P(1,4),
由B,C两点坐标可求直线BC解析式为y=-x+3,
设过点P与直线BC平行的直线为:y=-x+b′,
将点P(1,4)代入,得y=-x+5,
则过点P与直线BC平行的直线与抛物线联立,有则存在点Q,
-x2+2x+3=-x+5,
即x2-3x+2=0,
解得x=1或x=2,
代入直线则得点(1,4)或(2,3),
已知点P(1,4),
所以点Q(2,3),

由对称轴及直线BC解析式可知M(1,2),PM=2,
设过P′(1,0)且与BC平行的直线为y=-x+f,
将P′代入,得y=-x+1,
联立
|
|
|
∴Q(2,3)或(
3-
| ||
| 2 |
-1+
| ||
| 2 |
3+
| ||
| 2 |
-1-
| ||
| 2 |
(3)由题意求得直线BC代入x=1,则y=2,
∴M(1,2),
由点M,P的坐标可知:
点R存在,即过点M平行于x轴的直线,
则代入y=2,x2-2x-1=0,
解得x=1-
| 2 |
| 2 |
即点R(1+
| 2 |

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
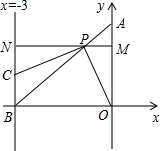
 ,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.
,求出点P的坐标,并求出梯形的面积;若不存在,请说明理由.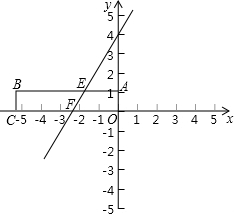
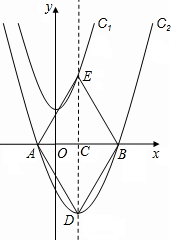

 角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.
角形?如果可能,求出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.