题目内容
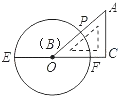
【题目】如图,AB是半圆O的直径,C为半圆上一点,N是线段BC上一点(不与B﹑C重合),过N作AB的垂线交AB于M,交AC的延长线于E,过C点作半圆O的切线交EM于F,若NC:CF=3:2,则sinB= .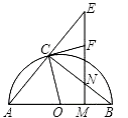
【答案】![]()
【解析】由题意,NC:CF=3:2,设NC=3x,则CF=2x,
∵AB为直径,
∴BC⊥AE,
∵CF为⊙O的切线,
∴OC⊥CF,
∵∠OCB+∠BCF=∠BCF+∠ECF=90°,
∴∠OCB=∠ECF,同理可证∠B=∠E,
∵OB=OC,
∴∠OCB=∠B,
∴∠ECF=∠E,则EF=CF=2x,
同理可证∠FCN=∠FNC,则FN=CF=2x,
∴在Rt△CEN中,sinE= ![]() =
= ![]() =
= ![]() ,∴sinB=sinE=
,∴sinB=sinE= ![]() .
.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目