题目内容
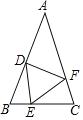
【题目】如图,在△ABC中AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)猜想:当∠A为多少度时,∠DEF=60°?请说明理由。
【答案】见解析
【解析】(1)通过全等三角形的判定定理SAS证得△DBE≌△RCF,由“全等三角形的对应边相等”推知DE=EF,所以△DEF是等腰三角形;
(2)由等腰△ABC的性质求得∠B=∠C=![]() (180°-40°)=70°,所以根据三角形内角和定理推知∠BDE+∠DEB=110°;再结合△DBE≌△ECF的对应角相等:∠BDE=∠FEC,故∠FEC+∠DEB=110°,易求∠DEF=70°;
(180°-40°)=70°,所以根据三角形内角和定理推知∠BDE+∠DEB=110°;再结合△DBE≌△ECF的对应角相等:∠BDE=∠FEC,故∠FEC+∠DEB=110°,易求∠DEF=70°;
(3)由(2)知,∠DEF=∠B,于是得到∠B=60°,推出△ABC是等边三角形,于是得到结论.
解:(1)因为AB=AC,所以∠B=∠C.
因为AD+EC=AB,AD+DB=AB,
所以BD=EC.
在△DBE和 △ECF中,因为BE=CF,∠B=∠C,BD=EC,
所以△DBE≌△ECF(SAS).
所以DE=EF.
所以△DEF是等腰三角形.
(2)因为∠A=40°,∠B=∠C,
所以∠B=∠C=70°.
因为△DBE≌△ECF,所以∠BDE=∠CEF.
因为∠DEC=∠DEF+∠FEC=∠B+∠BDE,
所以∠DEF=∠B.所以∠DEF=70°,
(3)当∠A为60°时,∠DEF=60°.理由如下:
由(2)知∠DEF=∠B.
若∠DEF=60°,则∠B=60°.
因为AB=AC,所以∠ABC是等边三角形.
所以∠A=60°.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目